Years
>
Year 10>
Fractions>
Order of Operations Involving Fractions>
Order of Operations Involving Fractions 2Order of Operations Involving Fractions 2
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 3 questions completed
Questions:
- 1
- 2
- 3
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- Answered
- Review
-
Question 1 of 3
1. Question
Solve the following.`3/4xx2/3+(3-2/3)`Hint
Help VideoCorrect
Great Work!
Incorrect
Order of Operations (BODMAS)
B – Bracket
O – Over (Powers, Exponents)
D – Division
M – Multiplication
A – Addition
S – SubtractionTransforming an Improper to Mixed Fraction
$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}=\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$`(``b``-:``c``)=``Q` and `R` is the remainderAccording to BODMAS, Bracket is prioritized over Multiplication, then followed by Addition.Ignore the other operations for now and only do the operation inside the bracket, which is subtraction.$$\color{#9E9E9E}{\frac{3}{4}\times\frac{2}{3}+}\color{#00880A}{\left({3-\frac{2}{3}}\right)}$$ First, make `3` into a fraction. Recall that all whole numbers has `1` as a denominator`3` `=` `3/1` To proceed with Subtraction, find the `LCD` of `1` and `3`Multiples of `1`:$$1\;\;2\;\;\color{#004ec4}{3}\;\;4\;\;5$$Multiples of `3`:$$\color{#004ec4}{3}\;\;6\;\;9\;\;12\;\;15$$The `LCD` of `1` and `3` is `3`Use the `LCD` as the denominator and then subtract.`3/1-2/3` `=` $$\frac{(\color{#004ec4}{3}\div1)\times3}{\color{#004ec4}{3}}-\frac{(\color{#004ec4}{3}\div3)\times2}{\color{#004ec4}{3}}$$ `=` `(3xx3)/3-(1xx2)/3` `=` `9/2-2/3` `=` `7/3` Next, ignore the addition for now and only do Multiplication.$$\color{#CC0000}{\frac{3}{4}\times\frac{2}{3}}\color{#9E9E9E}{+\frac{7}{3}}$$ `=` $$\frac{6}{12}\color{#9E9E9E}{+\frac{7}{3}}$$ `=` $$\frac{1}{2}\color{#9E9E9E}{+\frac{7}{3}}$$ Simplify` Next, to proceed with Addition, find the `LCD` of `2` and `3`Multiples of `2`:$$2\;\;4\;\;\color{#004ec4}{6}\;\;8\;\;10$$Multiples of `3`:$$3\;\;\color{#004ec4}{6}\;\;9\;\;12\;\;15$$The `LCD` of `2` and `3` is `6`Use the `LCD` as the denominator and then add.`1/2+7/3` `=` $$\frac{(\color{#004ec4}{6}\div2)\times1}{\color{#004ec4}{6}}+\frac{(\color{#004ec4}{6}\div3)\times7}{\color{#004ec4}{6}}$$ `=` `(3xx1)/6+(2xx7)/6` `=` `3/6+14/6` `=` `17/6` Finally, convert the improper fraction into a mixed number.Arrange the numbers for long division
`6` goes into `17` two times. So write `2` above the line.
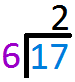Multiply `2` to `6` and write the answer below `17`
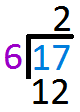Subtract `12` from `17` and write the answer one line below
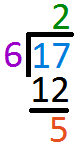Since `6` cannot go into `5` anymore, `5` is left as the Remainder and `2` is the QuotientSubstitute values into the given formula$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ `=` $$\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$ $$\frac{\color{#007DDC}{17}}{\color{#9a00c7}{6}}$$ `=` $$\color{#00880A}{2}\frac{\color{#e65021}{5}}{\color{#9a00c7}{6}}$$ `2 5/6` -
Question 2 of 3
2. Question
Solve the following.`4/5+3 2/3-:1/6`Hint
Help VideoCorrect
Keep Going!
Incorrect
Order of Operations (BODMAS)
B – Bracket
O – Over (Powers, Exponents)
D – Division
M – Multiplication
A – Addition
S – SubtractionTransforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{A})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ First, convert the mixed number in a fraction by multiplying the denominator by the whole number and then adding the numerator$$\color{#00880A}{3}\frac{\color{#007DDC}{2}}{\color{#9a00c7}{3}}$$ `=` $$\frac{(\color{#9a00c7}{3}\times\color{#00880A}{3})+\color{#007DDC}{2}}{\color{#9a00c7}{3}}$$ `=` $$\frac{9+2}{3}$$ `=` $$\frac{11}{3}$$ According to BODMAS, Division is prioritized over Addition.Ignore the addition for now and only do division.$$\color{#9E9E9E}{\frac{4}{5}+}\frac{11}{3}\div\frac{1}{6}$$ `=` $$\color{#9E9E9E}{\frac{4}{5}+}\color{#e85e00}{\frac{11}{3}\div\frac{6}{1}}$$ Find the reciprocal of `1/6` then proceed with multiplication `=` $$\color{#9E9E9E}{\frac{4}{5}+}\frac{66}{3}$$ `=` $$\color{#9E9E9E}{\frac{4}{5}+}22$$ Simplify Simply combine the two remaining values to make a mixed number`4/5+22` `=` `22 4/5` `22 4/5` -
Question 3 of 3
3. Question
Solve the following.`5/8+1 1/2-:1 1/3`Hint
Help VideoCorrect
Fantastic!
Incorrect
Transforming an Improper to Mixed Fraction
$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}=\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$`(``b``-:``c``)=``Q` and `R` is the remainderTransforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{A})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ Order of Operations (BODMAS)
B – Bracket
O – Over (Powers, Exponents)
D – Division
M – Multiplication
A – Addition
S – SubtractionFirst, convert the mixed numbers in fractions by multiplying the denominator by the whole number and then adding the numerator`1 1/2`$$\color{#00880A}{1}\frac{\color{#007DDC}{1}}{\color{#9a00c7}{2}}$$ `=` $$\frac{(\color{#9a00c7}{2}\times\color{#00880A}{1})+\color{#007DDC}{1}}{\color{#9a00c7}{2}}$$ `=` $$\frac{2+1}{2}$$ `=` $$\frac{3}{2}$$ `1 1/3`$$\color{#00880A}{1}\frac{\color{#007DDC}{1}}{\color{#9a00c7}{3}}$$ `=` $$\frac{(\color{#9a00c7}{3}\times\color{#00880A}{1})+\color{#007DDC}{1}}{\color{#9a00c7}{3}}$$ `=` $$\frac{3+1}{3}$$ `=` $$\frac{4}{3}$$ According to BODMAS, Division is prioritized over Addition.Ignore the addition for now and only do division.$$\color{#9E9E9E}{\frac{5}{8}+}\color{#e85e00}{\frac{3}{2}\div\frac{4}{3}}$$ `=` $$\color{#9E9E9E}{\frac{5}{8}+}\frac{3}{2}\times\frac{3}{4}$$ Find the reciprocal of `4/3` then proceed with multiplication `=` $$\color{#9E9E9E}{\frac{5}{8}+}\frac{9}{8}$$ Next, proceed with the AdditionSince the denominators of the remaining values are the same, add only the numerators$$\frac{5}{8}+\frac{9}{8}$$ `=` $$\frac{14}{8}$$ Finally, convert the improper fraction into a mixed number.Arrange the numbers for long division
`8` goes into `14` one time. So write `1` above the line.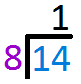
Multiply `1` to `8` and write the answer below `14`
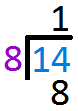Subtract `8` from `14` and write the answer one line below
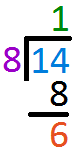Since `8` cannot go into `6` anymore, `6` is left as the Remainder and `1` is the QuotientSubstitute values into the given formula$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ `=` $$\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$ $$\frac{\color{#007DDC}{14}}{\color{#9a00c7}{8}}$$ `=` $$\color{#00880A}{1}\frac{\color{#e65021}{6}}{\color{#9a00c7}{8}}$$ `=` `1 3/4` Simplify the fraction `1 3/4`
Quizzes
- Shaded Fractions 1
- Shaded Fractions 2
- Equivalent Fractions 1
- Equivalent Fractions 2
- Equivalent Fractions 3
- Equivalent Fractions 4
- Simplify Fractions 1
- Simplify Fractions 2
- Simplify Fractions 3
- Find the Lowest Common Denominator
- Comparing Fractions 1
- Comparing Fractions 2
- Comparing Fractions 3
- Mixed and Improper Fractions 1
- Mixed and Improper Fractions 2
- Mixed and Improper Fractions 3
- Add and Subtract Fractions 1
- Add and Subtract Fractions 2
- Add and Subtract Fractions 3
- Add and Subtract Fractions 4
- Multiply and Divide Fractions 1
- Multiply and Divide Fractions 2
- Multiply and Divide Fractions 3
- Add and Subtract Mixed Numbers 1
- Add and Subtract Mixed Numbers 2
- Add and Subtract Mixed Numbers 3
- Multiply and Divide Mixed Numbers 1
- Multiply and Divide Mixed Numbers 2
- Multiply and Divide Mixed Numbers 3
- Multiply and Divide Mixed Numbers 4
- Fraction Word Problems: Addition and Subtraction 1
- Fraction Word Problems: Addition and Subtraction 2
- Fraction Word Problems: Addition and Subtraction 3
- Fraction Word Problems: Addition and Subtraction 4
- Fraction Word Problems: Multiplication and Division
- Find the Fraction of a Quantity
- Find the Quantity of a Quantity 1
- Find the Quantity of a Quantity 2
- Find the Fraction of a Quantity: Word Problems 1
- Find the Fraction of a Quantity: Word Problems 2
- Find the Fraction of a Quantity: Word Problems 3
- Find the Fraction of a Quantity: Word Problems 4
- Find the Quantity of a Quantity: Word Problems
- Order of Operations Involving Fractions 1
- Order of Operations Involving Fractions 2