Years
>
Year 8>
Fractions>
Multiply and Divide Mixed Numbers>
Multiply and Divide Mixed Numbers 3Multiply and Divide Mixed Numbers 3
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 4 questions completed
Questions:
- 1
- 2
- 3
- 4
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- Answered
- Review
-
Question 1 of 4
1. Question
Divide the following:`3 3/5-:9/10`- (4)
Hint
Help VideoCorrect
Keep Going!
Incorrect
Transforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{A})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ To divide fractions, flip the divisor and then multiply as normalFirst, convert the mixed numbers into improper formMultiply the denominator by the whole number and then add it to the numerator$$\color{#00880A}{3}\frac{\color{#007DDC}{3}}{\color{#9a00c7}{5}}\div\frac{9}{10}$$ `=` $$\frac{(\color{#9a00c7}{5}\times\color{#00880A}{3})+\color{#007DDC}{3}}{\color{#9a00c7}{5}} \div \frac{9}{10}$$ `=` `(15+3)/5 -: 9/10` `=` `18/5 -: 9/10` Now, get the reciprocal (flip) of the divisor`9/10` becomes `10/9` Proceed with multiplying this to the dividend.`18/5-:``9/10` `=` `18/5xx``10/9` `=` $$\frac{18\div\color{#CC0000}{9}}{5}\times\frac{10}{9\div\color{#CC0000}{9}}$$ Reduce the fractions `=` `2/5xx10/1` `=` $$\frac{2}{5\div\color{#CC0000}{5}}\times\frac{10\div\color{#CC0000}{5}}{1}$$ Reduce the fractions further `=` `2/1xx2/1` `=` `4/1` `=` `4` `4` -
Question 2 of 4
2. Question
Divide the following:`4 2/3-:7/8`Hint
Help VideoCorrect
Fantastic!
Incorrect
Transforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{A})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ Transforming an Improper to Mixed Fraction
$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}=\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$`(``b``-:``c``)=``Q` and `R` is the remainderTo divide fractions, flip the divisor and then multiply as normalFirst, convert the mixed numbers into improper formMultiply the denominator by the whole number and then add it to the numerator$$\color{#00880A}{4}\frac{\color{#007DDC}{2}}{\color{#9a00c7}{3}}\div\frac{7}{8}$$ `=` $$\frac{(\color{#9a00c7}{3}\times\color{#00880A}{4})+\color{#007DDC}{2}}{\color{#9a00c7}{3}} \div \frac{7}{8}$$ `=` `(12+2)/3 -: 7/8` `=` `14/3 -: 7/8` Now, get the reciprocal (flip) of the divisor`7/8` becomes `8/7` Proceed with multiplying this to the dividend.`14/3-:``7/8` `=` `14/3xx``8/7` `=` $$\frac{14\div\color{#CC0000}{7}}{3}\times\frac{8}{7\div\color{#CC0000}{7}}$$ Reduce the fractions `=` `2/3xx8/1` `=` `16/3` Convert the fraction from improper to mixedStart by dividing the numerator by the denominatorArrange the numbers for long division
`3` goes into `16` five times. So write `5` above the line.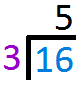
Multiply `5` to `3` and write the answer below `15`
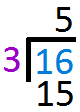Subtract `15` from `16` and write the answer one line below
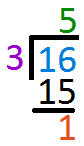Since `3` cannot go into `1` anymore, `1` is left as the Remainder and `5` is the QuotientSubstitute values into the given formula$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ `=` $$\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$ $$\frac{\color{#007DDC}{16}}{\color{#9a00c7}{3}}$$ `=` $$\color{#00880A}{5}\frac{\color{#e65021}{1}}{\color{#9a00c7}{3}}$$ `5 1/3` -
Question 3 of 4
3. Question
Divide the following:`2 3/10-:2 4/5`Write fractions in the format “a/b”- (23/28)
Hint
Help VideoCorrect
Excellent!
Incorrect
Transforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{A})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ To divide fractions, flip the divisor and then multiply as normalFirst, convert the mixed numbers into improper formMultiply the denominator by the whole number and then add it to the numerator$$\color{#00880A}{2}\frac{\color{#007DDC}{3}}{\color{#9a00c7}{10}}\div\color{#00880A}{2}\frac{\color{#007DDC}{4}}{\color{#9a00c7}{5}}$$ `=` $$\frac{(\color{#9a00c7}{10}\times\color{#00880A}{2})+\color{#007DDC}{3}}{\color{#9a00c7}{10}} \div \frac{(\color{#9a00c7}{5}\times\color{#00880A}{2})+\color{#007DDC}{4}}{\color{#9a00c7}{5}}$$ `=` `(20+3)/10 -: (10+4)/5` `=` `23/10 -: 14/5` Now, get the reciprocal (flip) of the divisor`14/5` becomes `5/14` Proceed with multiplying this to the dividend.`23/10-:``14/5` `=` `23/10xx``5/14` `=` $$\frac{23}{10\div\color{#CC0000}{5}}\times\frac{5\div\color{#CC0000}{5}}{14}$$ Reduce the fractions `=` `23/2xx1/14` `=` `23/28` `23/28` -
Question 4 of 4
4. Question
Divide the following:`10 1/2-:4`Hint
Help VideoCorrect
Well Done!
Incorrect
Transforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{A})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ Transforming an Improper to Mixed Fraction
$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}=\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$`(``b``-:``c``)=``Q` and `R` is the remainderTo divide fractions, flip the divisor and then multiply as normalFirst, convert the mixed numbers into improper formMultiply the denominator by the whole number and then add it to the numerator$$\color{#00880A}{10}\frac{\color{#007DDC}{1}}{\color{#9a00c7}{2}}\div4$$ `=` $$\frac{(\color{#9a00c7}{2}\times\color{#00880A}{10})+\color{#007DDC}{1}}{\color{#9a00c7}{2}} \div \frac{4}{1}$$ `=` `(20+1)/2 -: 4/1` `=` `21/2 -: 4/1` Now, get the reciprocal (flip) of the divisor`4/1` becomes `1/4` Proceed with multiplying this to the dividend.`21/2 -:``4/1` `=` `21/2xx``1/4` `=` `21/8` Convert the fraction from improper to mixedStart by dividing the numerator by the denominatorArrange the numbers for long division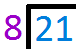
`8` goes into `21` two times. So write `2` above the line.
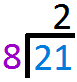Multiply `2` to `8` and write the answer below `21`
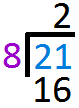Subtract `16` from `21` and write the answer one line below
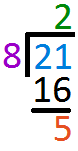Since `8` cannot go into `5` anymore, `5` is left as the Remainder and `2` is the QuotientSubstitute values into the given formula$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ `=` $$\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$ $$\frac{\color{#007DDC}{21}}{\color{#9a00c7}{8}}$$ `=` $$\color{#00880A}{2}\frac{\color{#e65021}{5}}{\color{#9a00c7}{8}}$$ `2 5/8`
Quizzes
- Shaded Fractions 1
- Shaded Fractions 2
- Equivalent Fractions 1
- Equivalent Fractions 2
- Equivalent Fractions 3
- Equivalent Fractions 4
- Simplify Fractions 1
- Simplify Fractions 2
- Simplify Fractions 3
- Find the Lowest Common Denominator
- Comparing Fractions 1
- Comparing Fractions 2
- Comparing Fractions 3
- Mixed and Improper Fractions 1
- Mixed and Improper Fractions 2
- Mixed and Improper Fractions 3
- Add and Subtract Fractions 1
- Add and Subtract Fractions 2
- Add and Subtract Fractions 3
- Add and Subtract Fractions 4
- Multiply and Divide Fractions 1
- Multiply and Divide Fractions 2
- Multiply and Divide Fractions 3
- Add and Subtract Mixed Numbers 1
- Add and Subtract Mixed Numbers 2
- Add and Subtract Mixed Numbers 3
- Multiply and Divide Mixed Numbers 1
- Multiply and Divide Mixed Numbers 2
- Multiply and Divide Mixed Numbers 3
- Multiply and Divide Mixed Numbers 4
- Fraction Word Problems: Addition and Subtraction 1
- Fraction Word Problems: Addition and Subtraction 2
- Fraction Word Problems: Addition and Subtraction 3
- Fraction Word Problems: Addition and Subtraction 4
- Fraction Word Problems: Multiplication and Division
- Find the Fraction of a Quantity
- Find the Quantity of a Quantity 1
- Find the Quantity of a Quantity 2
- Find the Fraction of a Quantity: Word Problems 1
- Find the Fraction of a Quantity: Word Problems 2
- Find the Fraction of a Quantity: Word Problems 3
- Find the Fraction of a Quantity: Word Problems 4
- Find the Quantity of a Quantity: Word Problems
- Order of Operations Involving Fractions 1
- Order of Operations Involving Fractions 2