Graph Linear Inequalities 2
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 7 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Answered
- Review
-
Question 1 of 7
1. Question
Graph `x gt 5`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `x=5`
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``x` `>` `5` `0` `>` `5` Plug in `0` as `x` The inequality is not true, so we will shade the side of the line which does not include the origin.Now we can graph the inequality.`gt` means we must use a dashed line when graphing `x gt 5`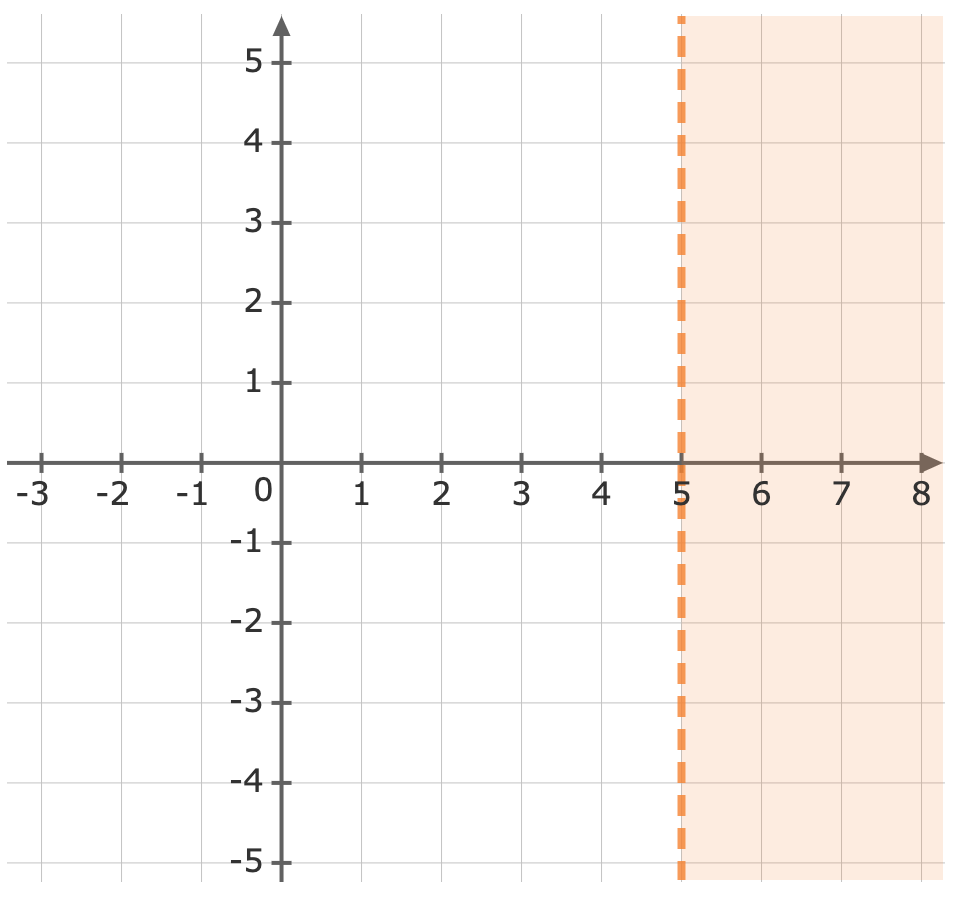
-
Question 2 of 7
2. Question
Graph `y lt 3`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `y=3`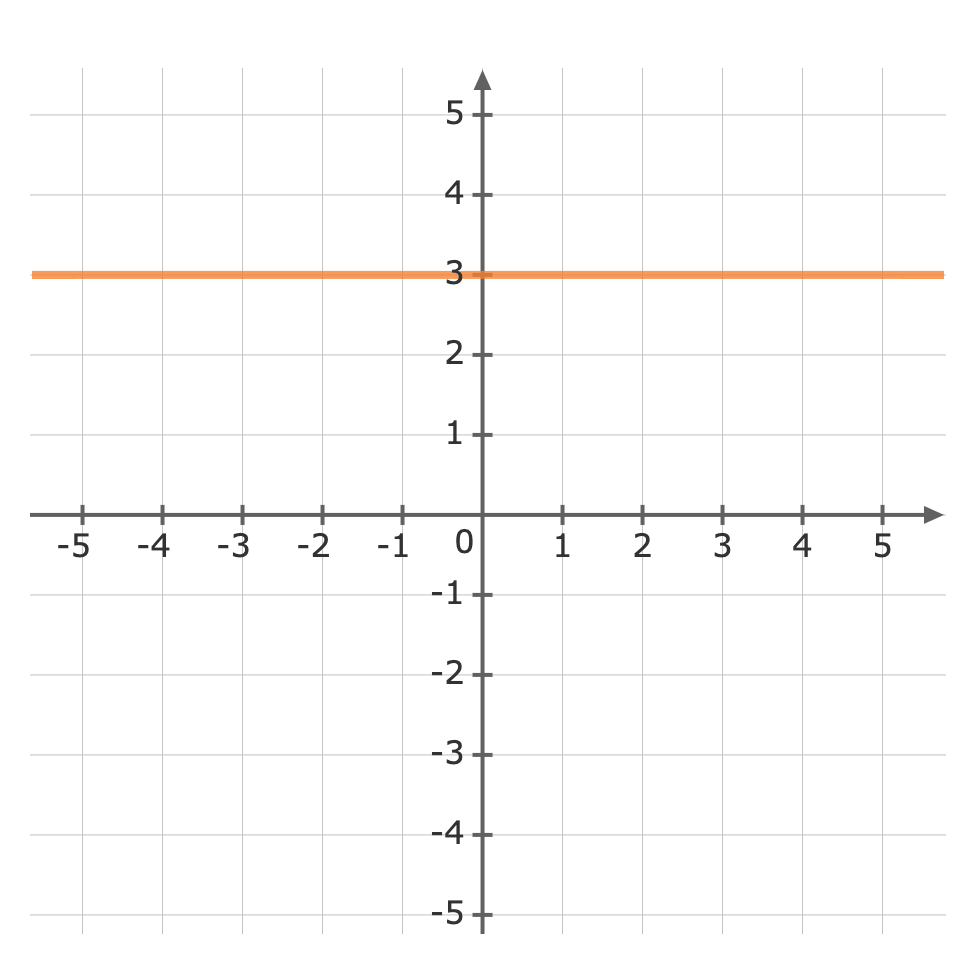
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``y` `<` `5` `0` `<` `5` Plug in `0` as `y` The inequality is true, so we will shade the side of the line which includes the origin.Now we can graph the inequality.`lt` means we must use a dashed line when graphing `y lt 3`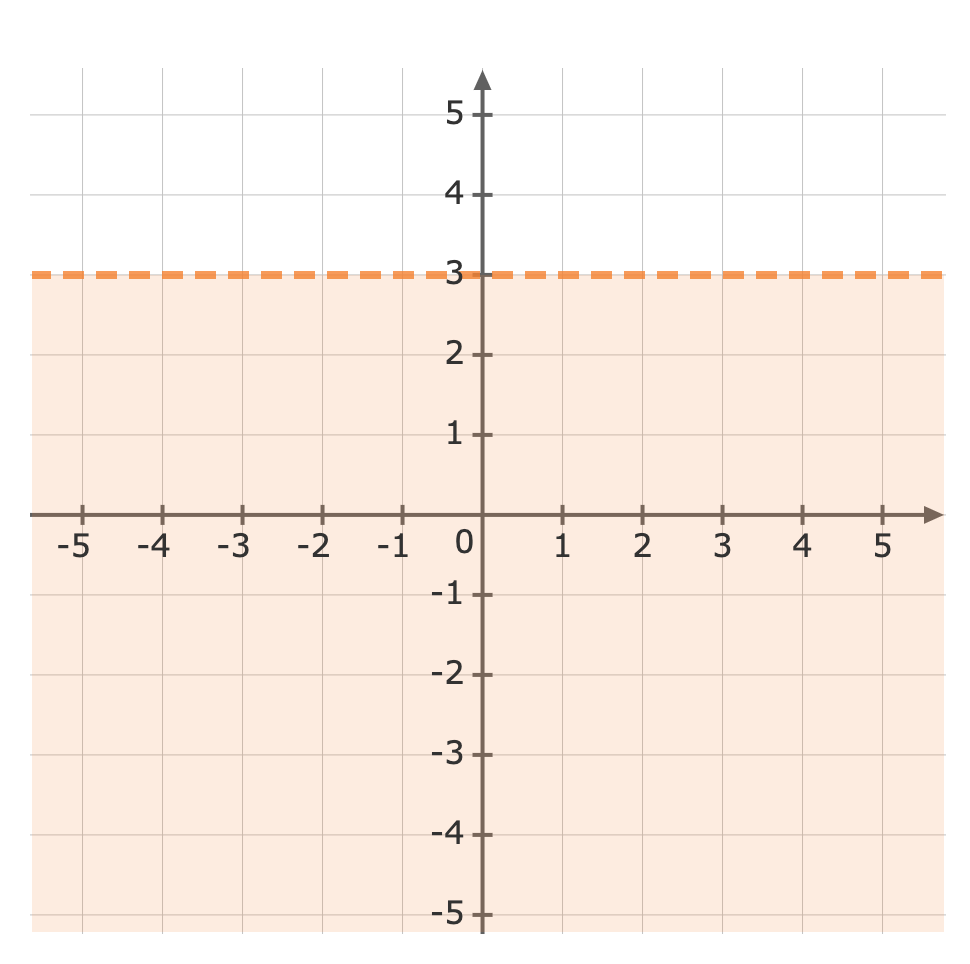
-
Question 3 of 7
3. Question
Graph `x ge 2`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `x=2`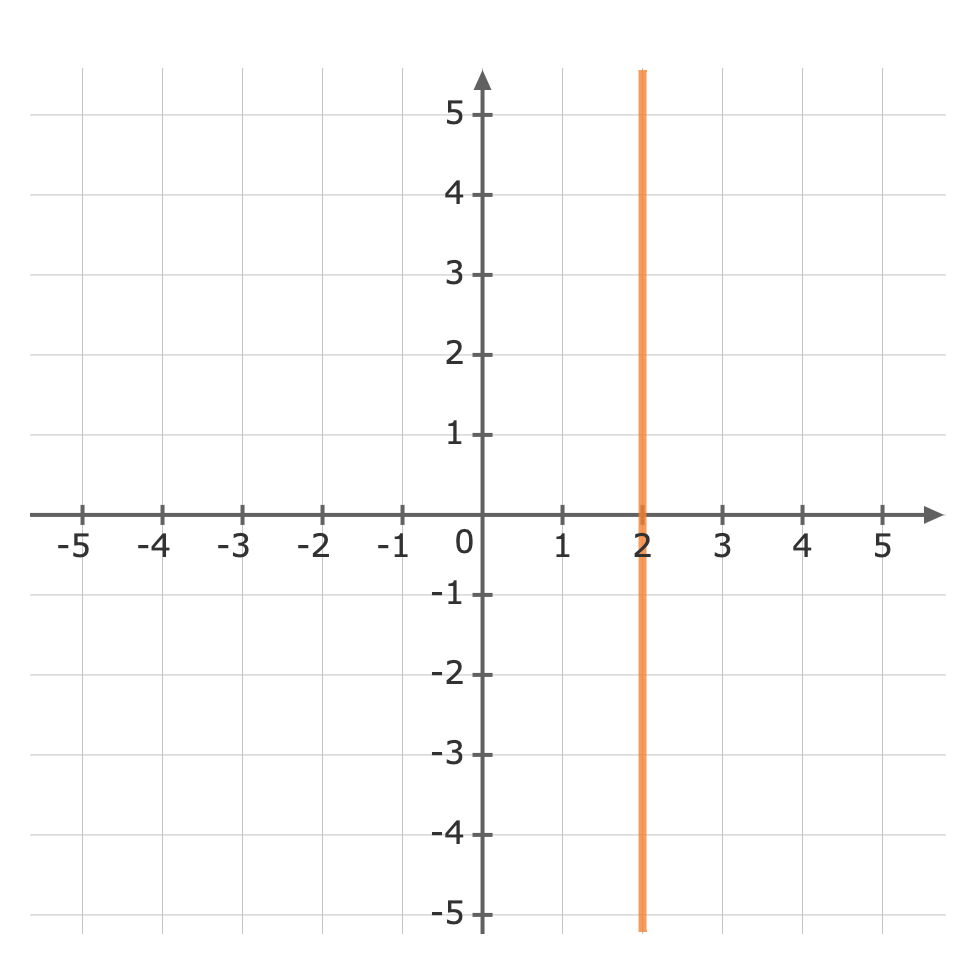
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``x` `ge` `2` `0` `ge` `2` Plug in `0` as `x` The inequality is not true, so we will shade the side of the line which does not include the origin.Now we can graph the inequality.`ge` means we must use a solid line when graphing `x ge 2`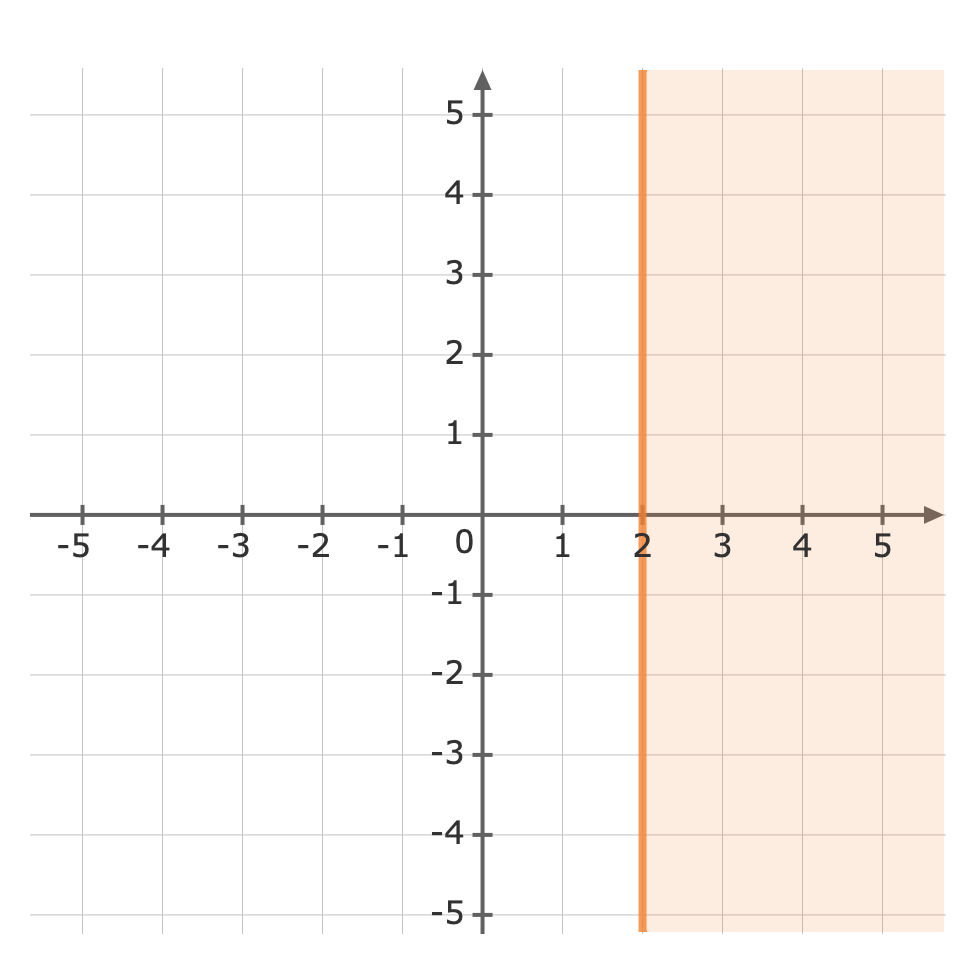
-
Question 4 of 7
4. Question
Graph `x ge 4`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `x=4`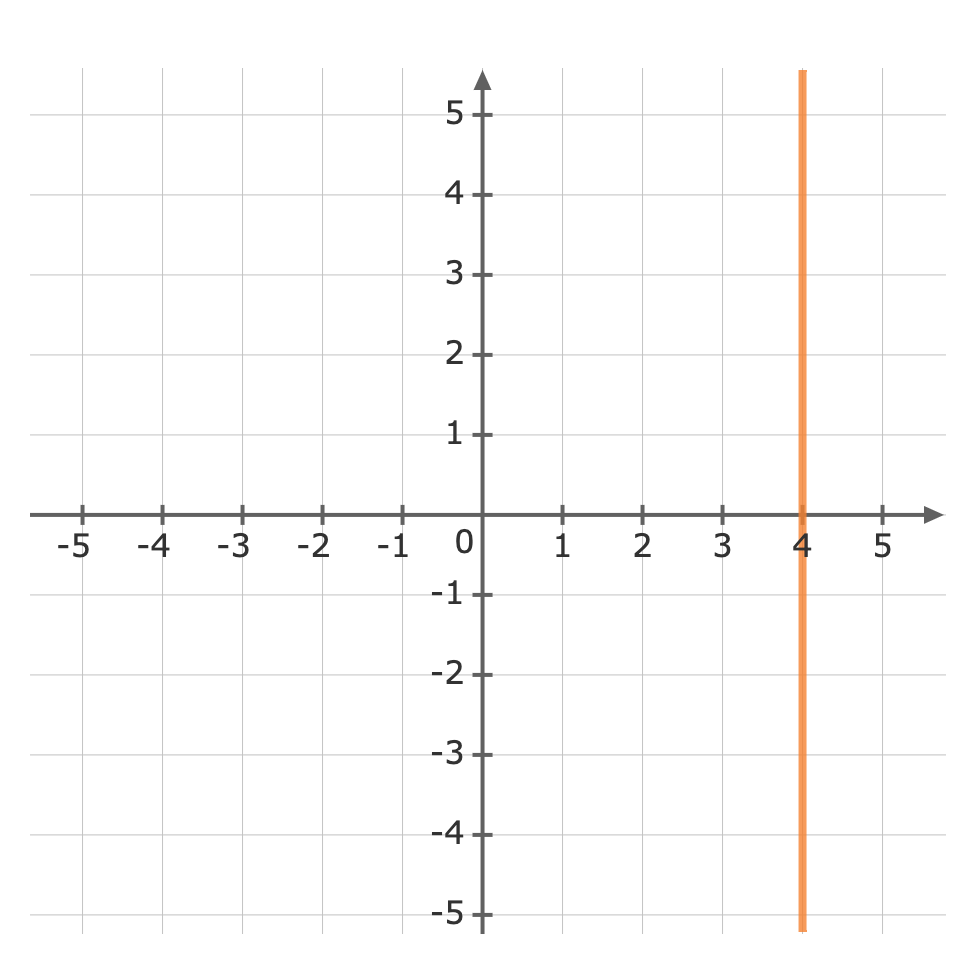
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``x` `ge` `4` `0` `ge` `4` Plug in `0` as `x` The inequality is not true, so we will shade the side of the line which does not include the origin.Now we can graph the inequality.`ge` means we must use a solid line when graphing `x ge 4`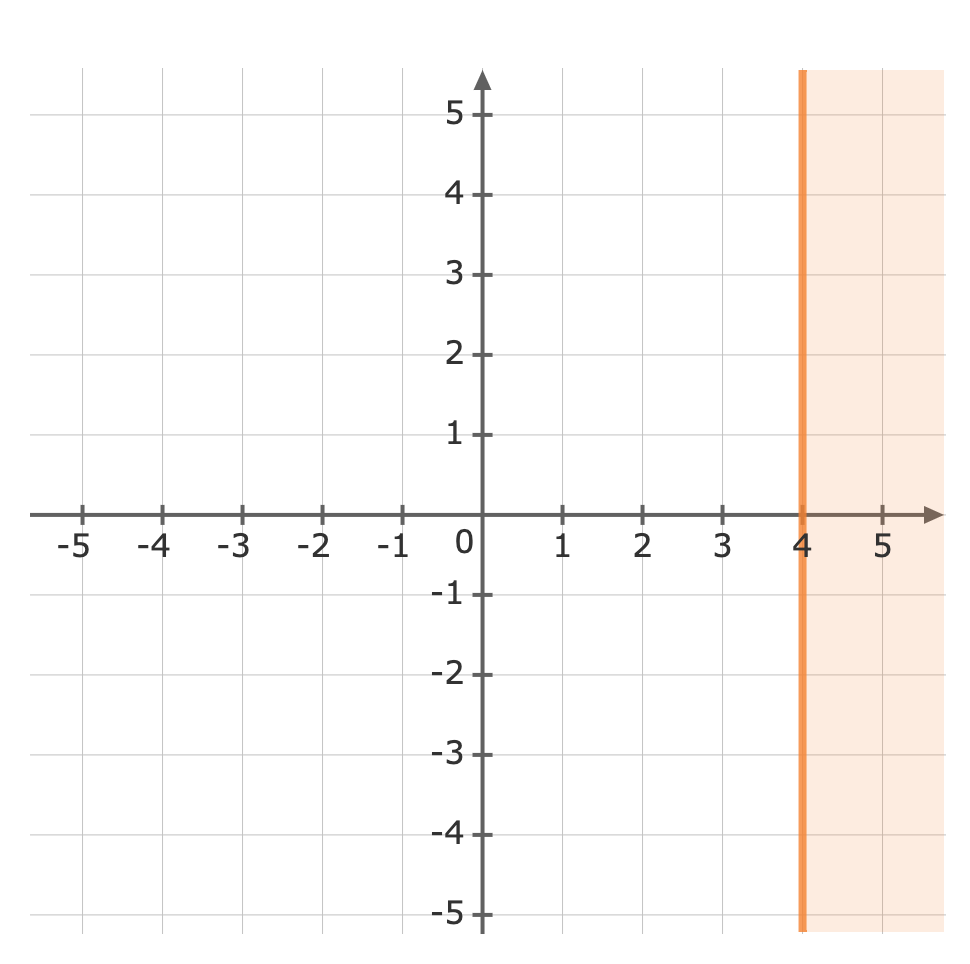
-
Question 5 of 7
5. Question
Graph `y ge -3`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `y=-3`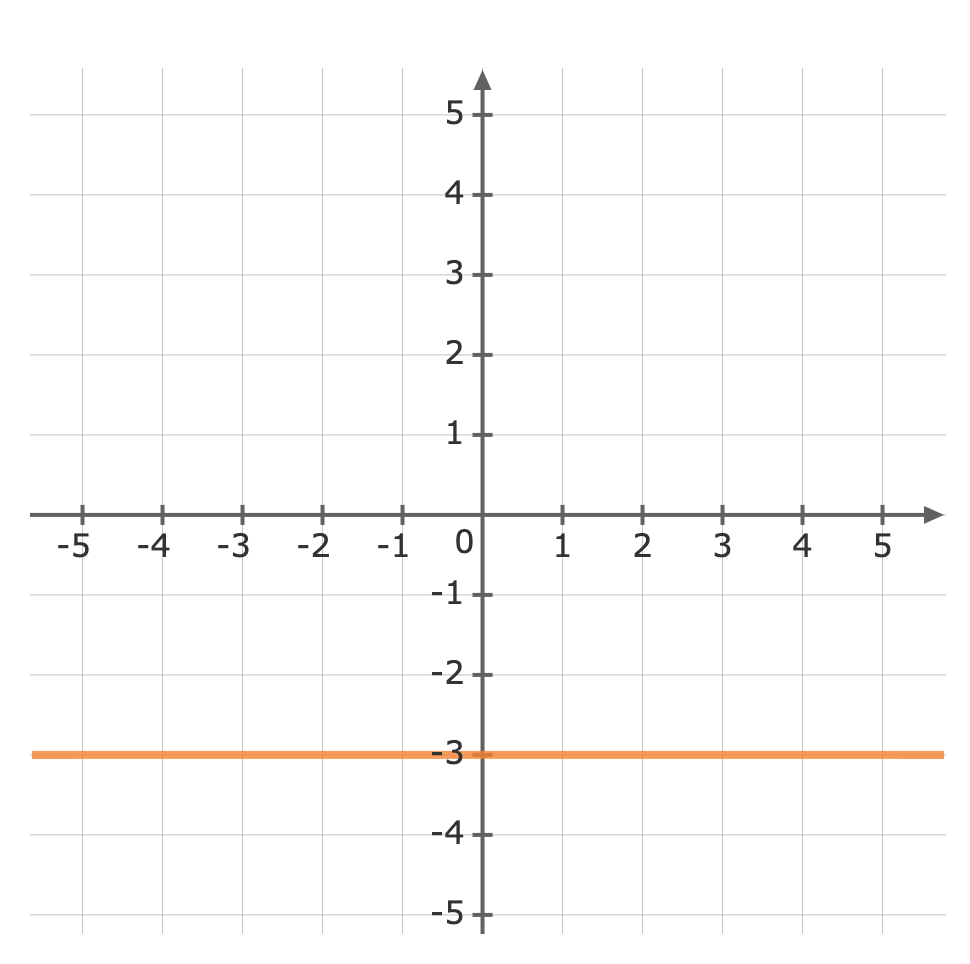
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``y` `ge` `-3` `0` `ge` `-3` Plug in `0` as `y` The inequality is true, so we will shade the side of the line which includes the origin.Now we can graph the inequality.`ge` means we must use a solid line when graphing `y ge -3`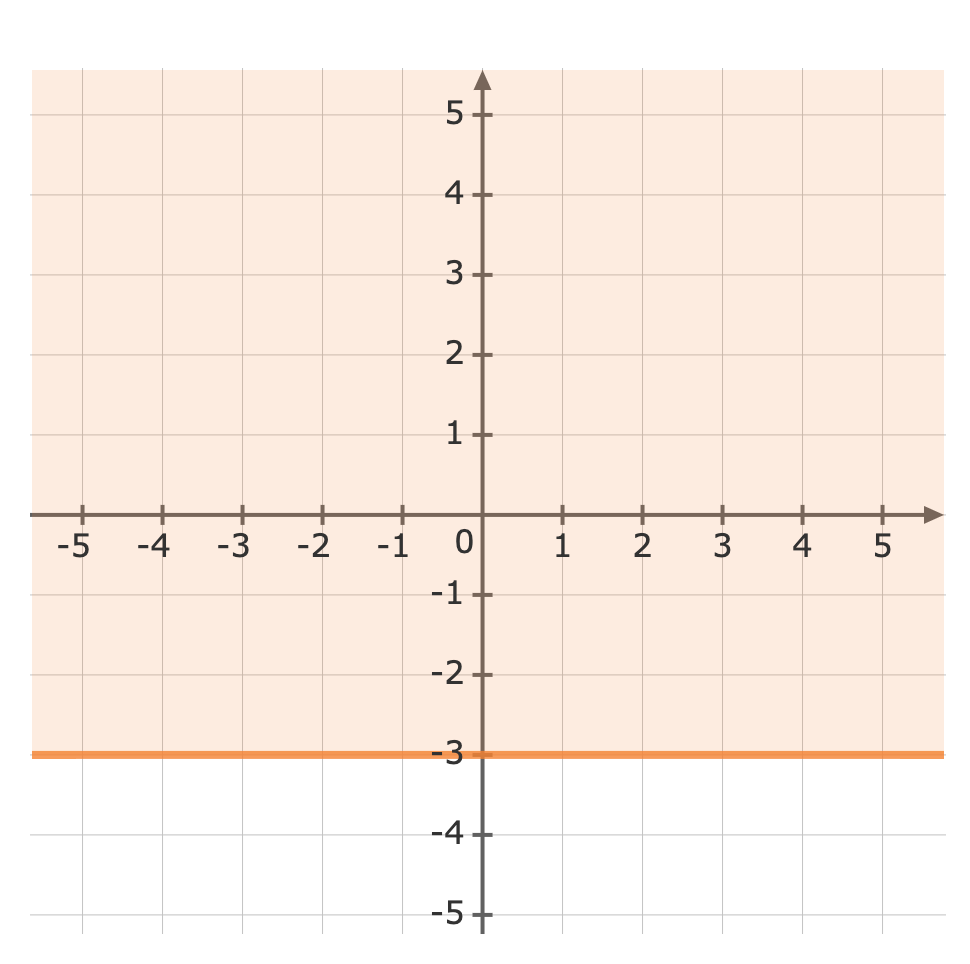
-
Question 6 of 7
6. Question
Graph `y gt 2x-1`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `y=2x-1`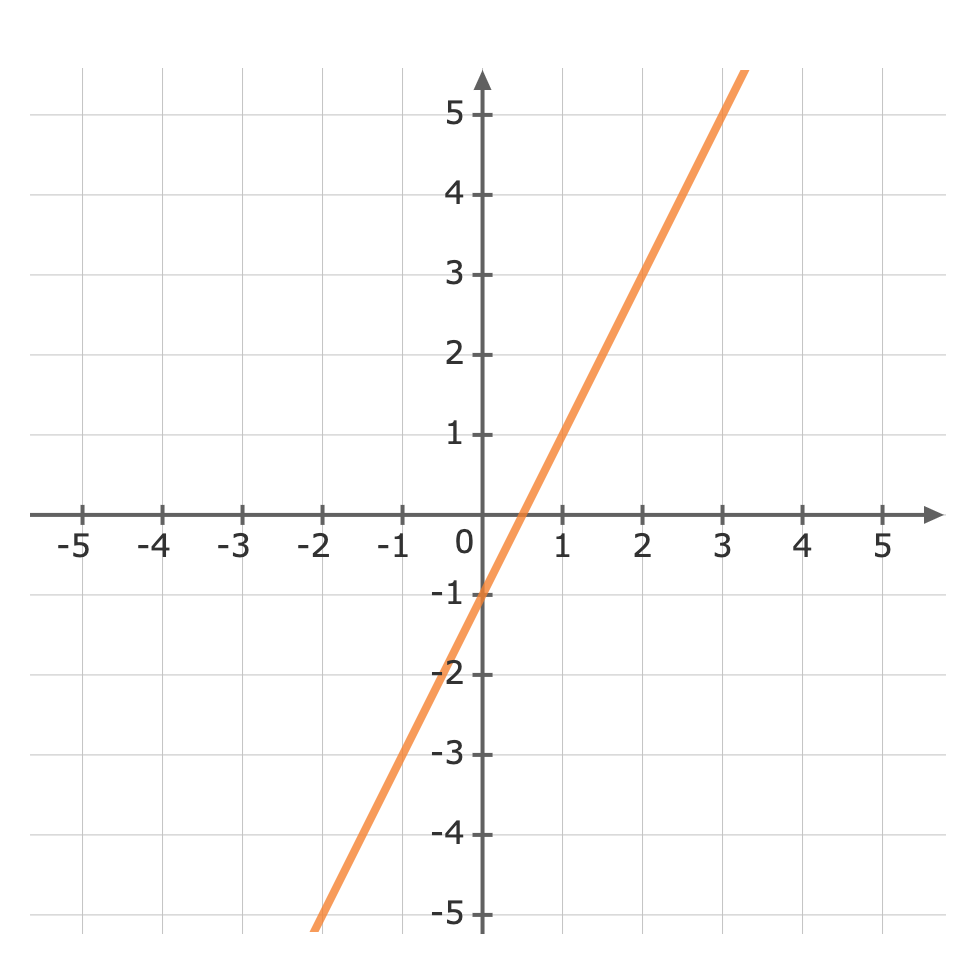
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``y` `gt` `2x-1` `0` `gt` `2 color(darkviolet)((0))-1` Plug in `0` as `x` and `y` `0` `gt` `-1` Simplify The inequality is true, so we will shade the side of the line which includes the origin.Now we can graph the inequality.`gt` means we must use a dashed line when graphing `y gt 2x-1`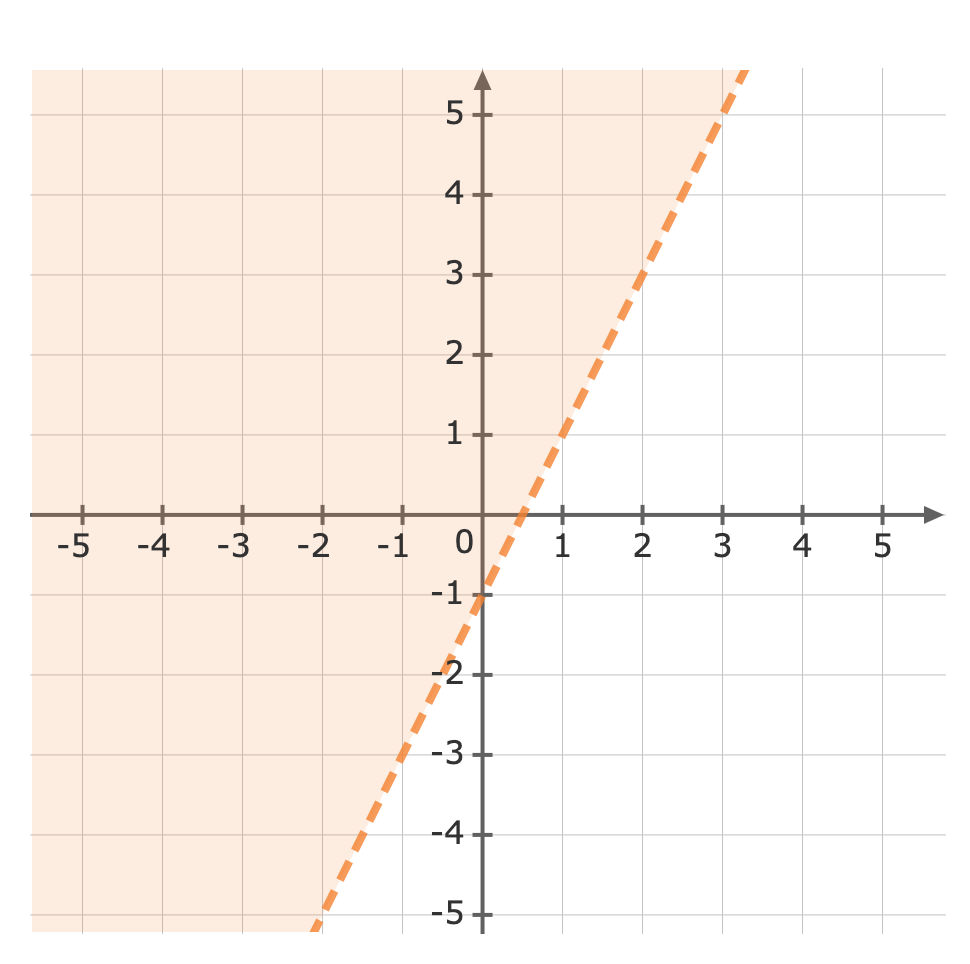
-
Question 7 of 7
7. Question
Graph `y gt 3x+1`
Correct
Keep Going!
Incorrect
Remember the following notations when graphing inequalities.Symbol Solid / Dotted `<` Dotted Line `>` Dotted Line `≤` Solid Line `≥` Solid Line First, treat the inequality sign as an equals sign and plot the curve.Graph the line `y=3x+1`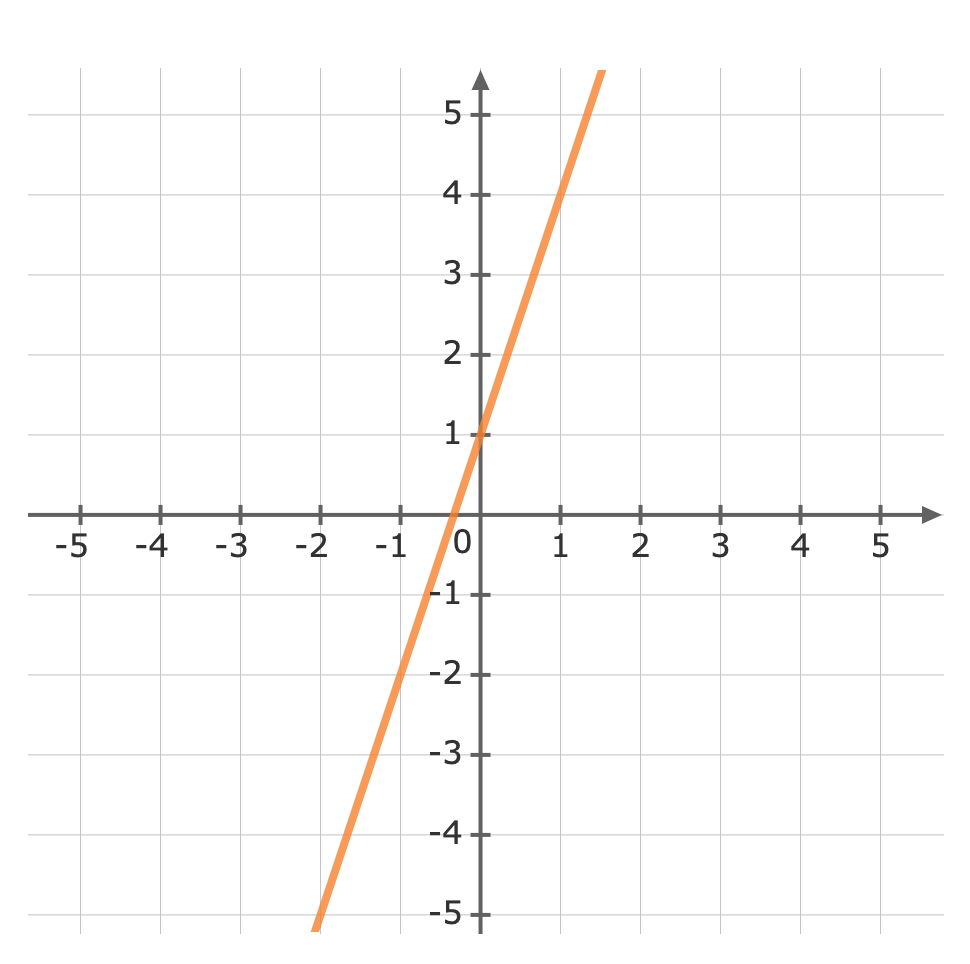
Use a test point to see which side of the line is to be shaded. We can try the origin, `(color(darkviolet)(0),0)``y` `gt` `3x+1` `0` `gt` `3 color(darkviolet)((0))+1` Plug in `0` as `x` and `y` `0` `gt` `1` Simplify The inequality is false, so we will shade the side of the line which does not include the origin.Now we can graph the inequality.`gt` means we must use a dashed line when graphing `y gt 3x+1`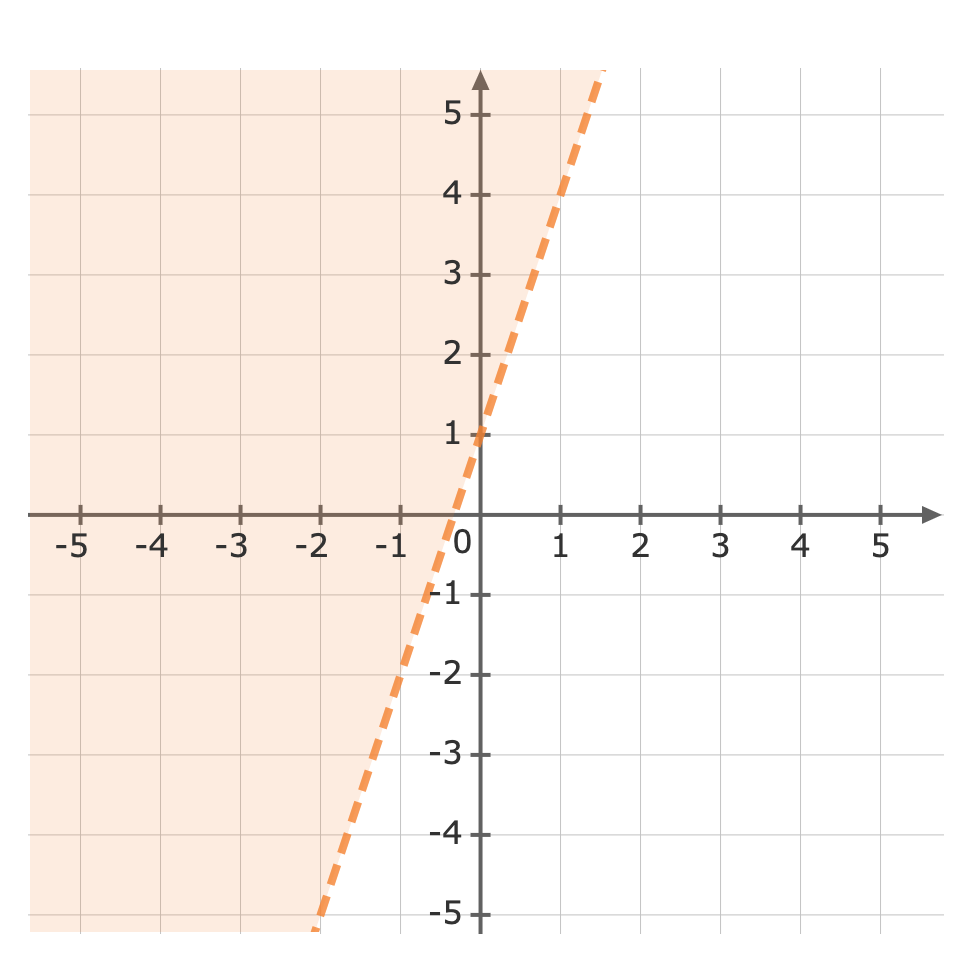
Quizzes
- Distance Between Two Points 1
- Distance Between Two Points 2
- Distance Between Two Points 3
- Midpoint of a Line 1
- Midpoint of a Line 2
- Midpoint of a Line 3
- Gradient of a Line 1
- Gradient of a Line 2
- Gradient Intercept Form: Graph an Equation 1
- Gradient Intercept Form: Graph an Equation 2
- Gradient Intercept Form: Write an Equation 1
- Determine if a Point Lies on a Line
- Graph Linear Inequalities 1
- Graph Linear Inequalities 2
- Convert Between General Form and Gradient Intercept Form 1
- Convert Between General Form and Gradient Intercept Form 2
- Point Gradient and Two Point Formula 1
- Point Gradient and Two Point Formula 2
- Parallel Lines 1
- Parallel Lines 2
- Perpendicular Lines 1
- Perpendicular Lines 2