Factor Theorem
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 2 questions completed
Questions:
- 1
- 2
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- Answered
- Review
-
Question 1 of 2
1. Question
Factorise`P(x)=x^3+x^2-14x-24`Hint
Help VideoCorrect
Well Done!
Incorrect
Long Division
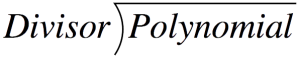 Use long division when a polynomial is divided by a binomial
Use long division when a polynomial is divided by a binomialFactor Theorem
factor `(P(x))/(x-a)` only if `P(a)=0`Find the first factor using Factor Theorem and trial and error.It is easier to try out numbers that divide to the constant term which is `-24`.`24` can be divided by: `+-` `1,2,3,4,6,8,12`Trying out `a=1`:`P(x)` `=` `x^3+x^2-14x-24` `P(a)` `=` `a^3+a^2-14a-24` Replace `x` with `a` `P(1)` `=` `1^3+1^2-14(1)-24` Substitute `a=1` `=` `1+1-14-24` `=` `-36` Since `P(1)≠0`, `(x-1)` is not a factor of the polynomialTrying out `a=2`:`P(x)` `=` `x^3+x^2-14x-24` `P(a)` `=` `a^3+a^2-14a-24` Replace `x` with `a` `P(2)` `=` `2^3+2^2-14(2)-24` Substitute `a=2` `=` `8+4-28-24` `=` `-40` Since `P(2)≠0`, `(x-2)` is not a factor of the polynomialTrying out `a=-3`:`P(x)` `=` `x^3+x^2-14x-24` `P(a)` `=` `a^3+a^2-14a-24` Replace `x` with `a` `P(-3)` `=` `(-3)^3+(-3)^2-14(-3)-24` Substitute `a=-3` `=` `-27+9+42-24` `=` `0` Since `P(-3)=0`, `(x+3)` is the first factor of the polynomialFind the second factor using Long Division.Substitute components into the formula$$\mathsf{P}$$(Polynomial) `=` `x^3+x^2-14x-24` $$\mathsf{Divisor}$$ `=` `x+3` 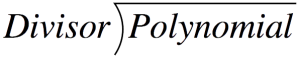
`=` Next, solve for each term of the quotientFirst term of the quotient:Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial`x^3dividex` `=` `x^2` Multiply `x^2` to the divisor. Place this under the Polynomial`x^2``(x+3)` `=` `x^3+3x^2` Subtract `x^3+3x^2` and write the difference one line belowDrop down `-14x` and repeat the process to get the second term of the quotientSecond term of the quotient:Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial`-2x^2dividex` `=` `-2x` Multiply `-2x` to the divisor. Place this one line below`-2x``(x+3)` `=` `-2x^2-6x` Subtract `-2x^2-6x` and write the difference one line belowDrop down `-24` and repeat the process to get the third term of the quotientThird term of the quotient:Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial`-8xdividex` `=` `-8` Multiply `-8` to the divisor. Place this under the Polynomial`-8``(x+3)` `=` `-8x-24` Subtract `-8x-24` and write the difference one line belowSince `r=0` and cannot be divided anymore, the quotient is `x^2-2x-8`So far, we have factored the polynomial as `(x+3)``(x^2-2x-8)`Factor out the polynomial further by applying cross method`(x+3)(x^2-2x-8)``(x+3)(x+2)(x-4)``(x+3)(x+2)(x-4)` -
Question 2 of 2
2. Question
Factorise`P(x)=2x^3-7x^2-10x+24`Hint
Help VideoCorrect
Correct!
Incorrect
Long Division
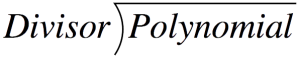 Use long division when a polynomial is divided by a binomial
Use long division when a polynomial is divided by a binomialFactor Theorem
factor `(P(x))/(x-a)` only if `P(a)=0`Find the first factor using Factor Theorem and trial and error.It is easier to try out numbers that divide to the constant term which is `24`.`24` can be divided by: `+-` `1,2,3,4,6,8,12`Trying out `a=2`:`P(x)` `=` `2x^3-7x^2-10x+24` `P(a)` `=` `2a^3-7a^2-10a+24` Replace `x` with `a` `P(2)` `=` `2(2)^3-7(2)^2-10(2)+24` Substitute `a=2` `=` `2(8)-7(4)-20+24` `=` `16-28-20+24` `=` `16-28-20+24` `=` `-8` Since `P(2)≠0`, `(x-2)` is not a factor of the polynomialTrying out `a=-2`:`P(x)` `=` `2x^3-7x^2-10x+24` `P(a)` `=` `2a^3-7a^2-10a+24` Replace `x` with `a` `P(-2)` `=` `2(-2)^3-7(-2)^2-10(-2)+24` Substitute `a=-2` `=` `2(-8)-7(4)+20+24` `=` `-16-28+20+24` `=` `0` Since `P(-2)=0`, `(x+2)` is the first factor of the polynomialFind the second factor using Long Division.Substitute components into the formula$$\mathsf{P}$$(Polynomial) `=` `2x^3-7x^2-10x+24` $$\mathsf{Divisor}$$ `=` `x+2` 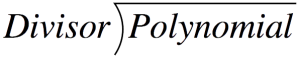
`=` 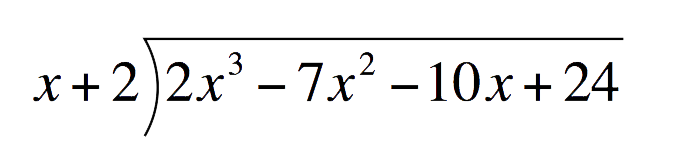 Next, solve for each term of the quotientFirst term of the quotient:Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial
Next, solve for each term of the quotientFirst term of the quotient:Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial`2x^3dividex` `=` `2x^2` 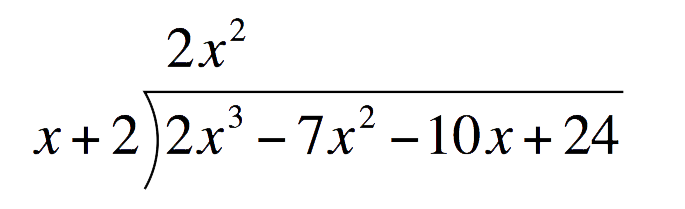 Multiply `2x^2` to the divisor. Place this under the Polynomial
Multiply `2x^2` to the divisor. Place this under the Polynomial`2x^2``(x+2)` `=` `2x^3+4x^2` 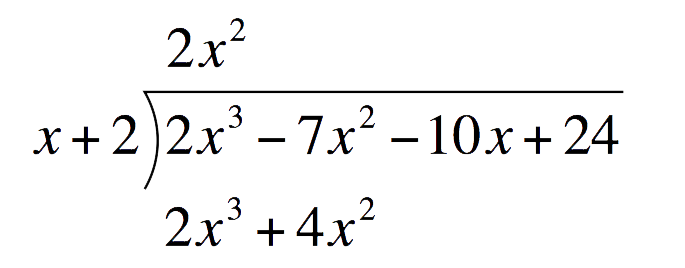 Subtract `2x^3+4x^2` and write the difference one line below
Subtract `2x^3+4x^2` and write the difference one line below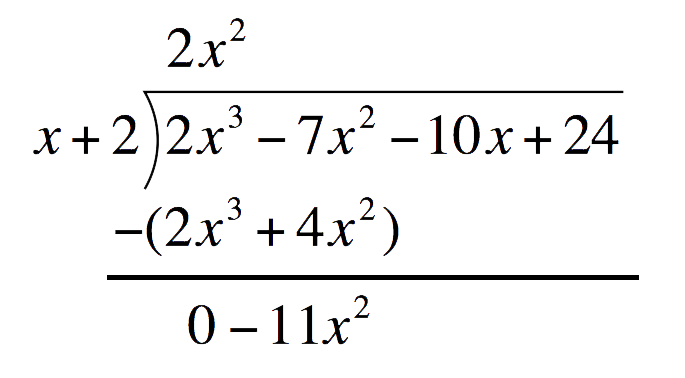 Drop down `-10x` and repeat the process to get the second term of the quotient
Drop down `-10x` and repeat the process to get the second term of the quotient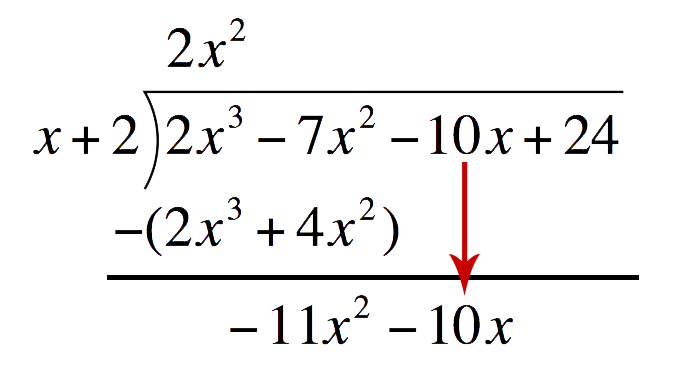 Second term of the quotient:Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial
Second term of the quotient:Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial`-11x^2dividex` `=` `-11x` 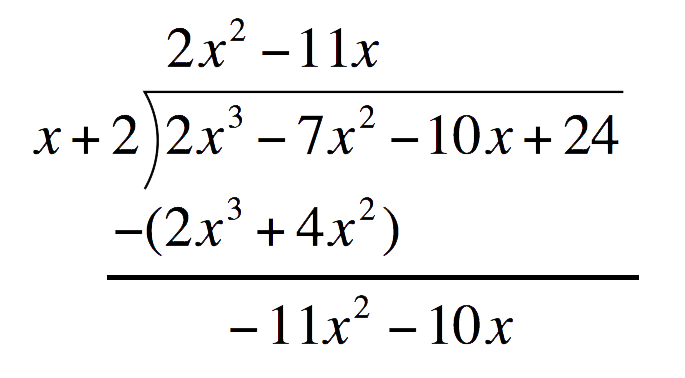 Multiply `-11x` to the divisor. Place this one line below
Multiply `-11x` to the divisor. Place this one line below`-11x``(x+2)` `=` `-11x^2-22x`  Subtract `-11x^2-22x` and write the difference one line below
Subtract `-11x^2-22x` and write the difference one line below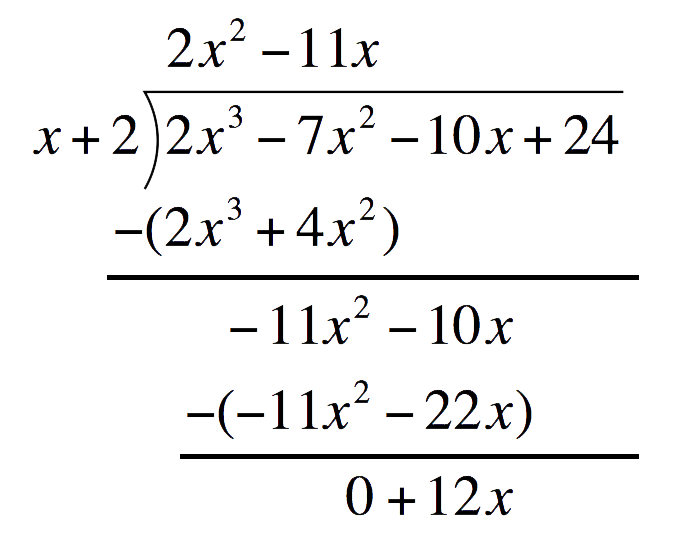 Drop down `24` and repeat the process to get the third term of the quotient
Drop down `24` and repeat the process to get the third term of the quotient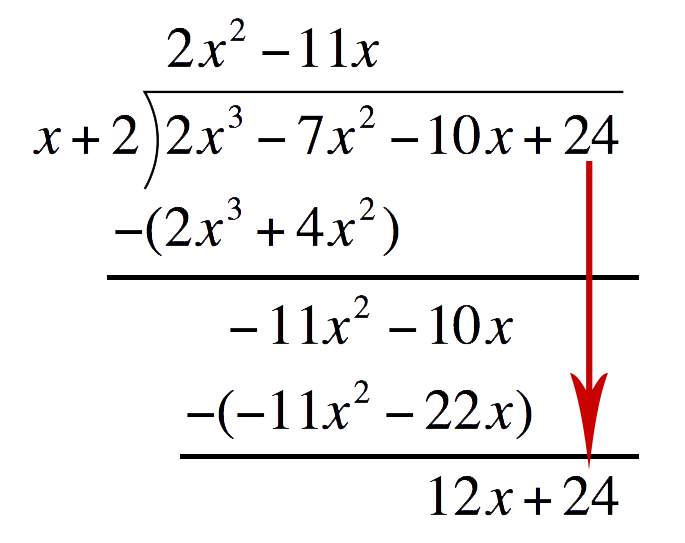 Third term of the quotient:Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial
Third term of the quotient:Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial`12xdividex` `=` `12` 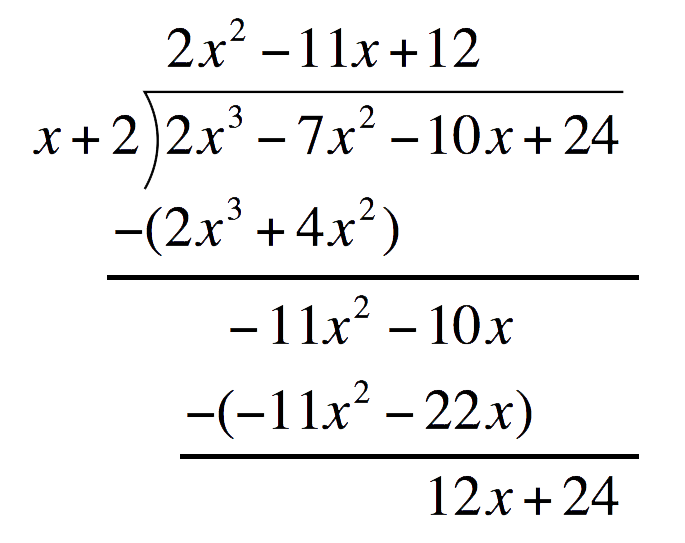 Multiply `12` to the divisor. Place this under the Polynomial
Multiply `12` to the divisor. Place this under the Polynomial`12``(x+2)` `=` `12x+24` 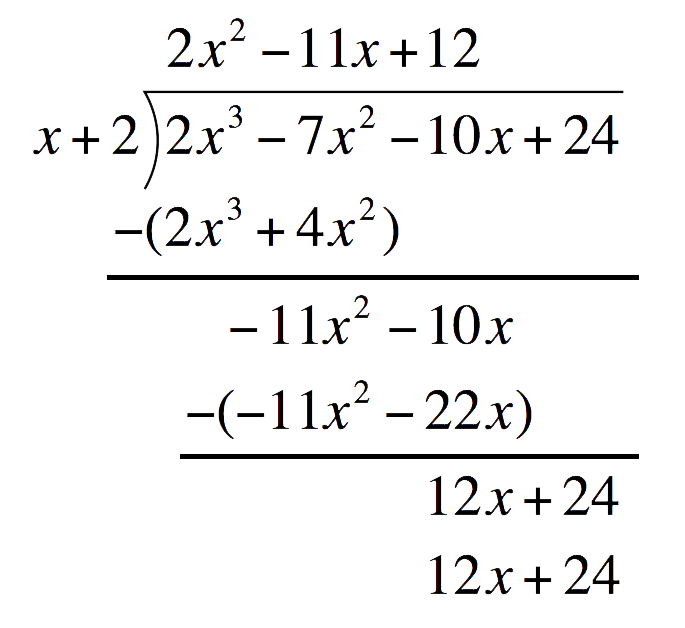 Subtract `12x+24` and write the difference one line below
Subtract `12x+24` and write the difference one line below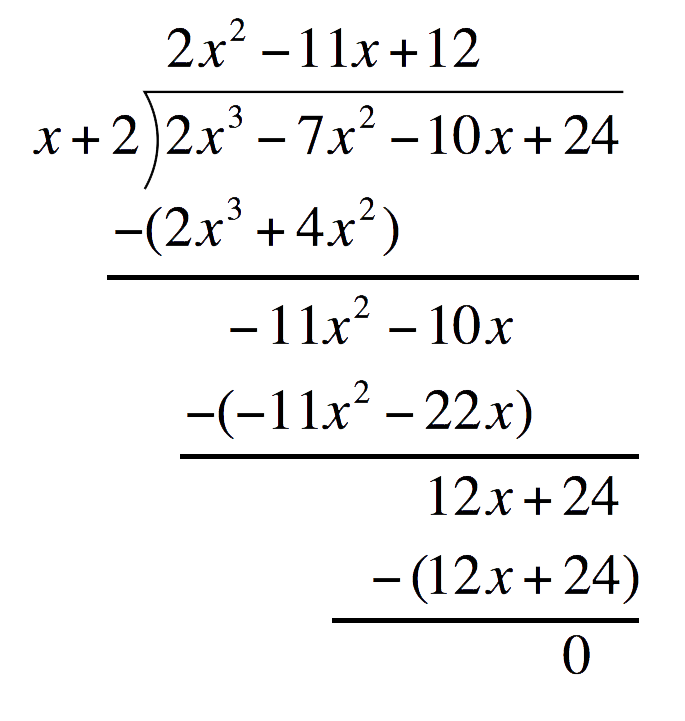 Since `r=0` and cannot be divided anymore, the quotient is `2x^2-11x+12`So far, we have factored the polynomial as `(x+2)``(2x^2-11x+12)`Factor out the polynomial further by applying cross method`(x+2)(2x^2-11x+12)``(x+2)(2x-3)(x-4)``(x+2)(2x-3)(x-4)`
Since `r=0` and cannot be divided anymore, the quotient is `2x^2-11x+12`So far, we have factored the polynomial as `(x+2)``(2x^2-11x+12)`Factor out the polynomial further by applying cross method`(x+2)(2x^2-11x+12)``(x+2)(2x-3)(x-4)``(x+2)(2x-3)(x-4)`
















