Working with Radial Surveys 1
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 6 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- Answered
- Review
-
Question 1 of 6
1. Question
From the radial survey below, find the area of `triangleAOB`: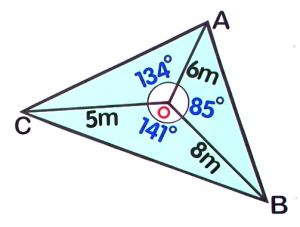
Round your answer to `3` decimal places- Area of `triangleAOB=` (23.909)`m^2`
Hint
Help VideoCorrect
Great Work!
Incorrect
Area of a Non-Right Angled Triangle
`A_triangle=1/2``a``b``sin``C`where:
`a` is the side opposite angle `A`
`b` is the side opposite angle `B`
`c` is the side opposite angle `C`A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.First, identify the known values of the triangle `AOB`.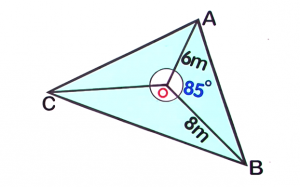
Now, substitute the known values to the formula and solve for the area.
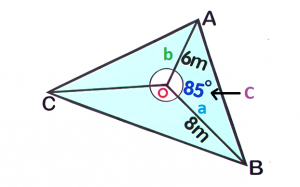`a=8m``b=6m``C=85°``A_triangle` `=` `1/2``a``b``sin``C` `=` `1/2(``8``)(``6``)sin``85°` Substitute the values `=` `1/2(48)sin85°` Evaluate `sin` `85` on your calculator `=` `24times0.9961947` `=` `23.909m^2` Round off to `3` decimal places `23.909m^2` -
Question 2 of 6
2. Question
From the radial survey below, find the area of `triangleBOC`:Round your answer to `3` decimal places- Area of `triangleBOC=` (12.586)`m^2`
Hint
Help VideoCorrect
Correct!
Incorrect
Area of a Non-Right Angled Triangle
`A_triangle=1/2``a``b``sin``C`where:
`a` is the side opposite angle `A`
`b` is the side opposite angle `B`
`c` is the side opposite angle `C`A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.First, identify the known values of the triangle `BOC`.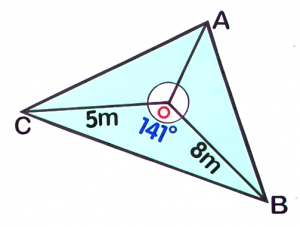
Now, substitute the known values to the formula and solve for the area.
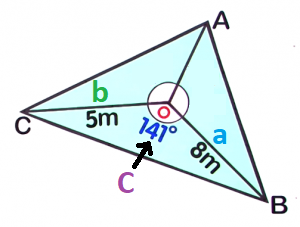`a=8m``b=5m``C=141°``A_triangle` `=` `1/2``a``b``sin``C` `=` `1/2(``8``)(``5``)sin``141°` Substitute the values `=` `1/2(40)sin141°` Evaluate `sin` `141` on your calculator `=` `20times0.62932` `=` `12.586m^2` Round off to `3` decimal places `12.586m^2` -
Question 3 of 6
3. Question
From the radial survey below, find the following:-
`(i)` Area of `triangleAOC=` (10.790)`m^2 (3` decimal places`)``(ii)` Total Area of `triangleABC=` (47.3)`m^2 (1` decimal place`)`
Hint
Help VideoCorrect
Well Done!
Incorrect
Area of a Non-Right Angled Triangle
`A_triangle=1/2``a``b``sin``C`where:
`a` is the side opposite angle `A`
`b` is the side opposite angle `B`
`c` is the side opposite angle `C`A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.`(i)` Area of `triangleAOC`First, identify the known values of the triangle `AOC`.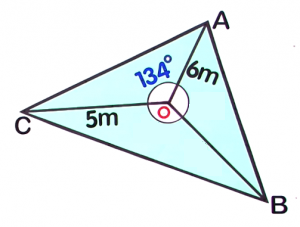
Now, substitute the known values to the formula and solve for the area.
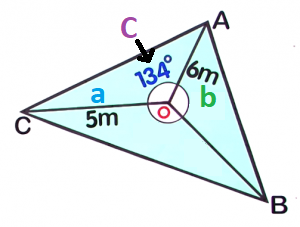`a=5m``b=6m``C=134°``A_triangle` `=` `1/2``a``b``sin``C` `=` `1/2(``5``)(``6``)sin``134°` Substitute the values `=` `1/2(30)sin134°` Evaluate `sin` `134` on your calculator `=` `15times0.7193398` `=` `10.790m^2` Round off to `3` decimal places `(ii)` Total Area of `triangleABC`Finally, add the area of triangles `AOB` (from Question `1`), `BOC` (from Question `2`) and `AOC`.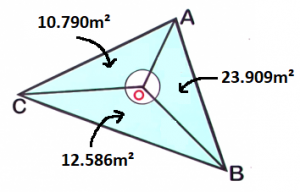
Total Area `=` `triangleAOB+triangleBOC+triangleAOC` `=` `23.909+12.586+10.790` Substitute the values `=` `47.285` Use the calculator `=` `47.3m^2` Rounded off to `1` decimal place `(i) 10.790m^2``(ii) 47.3m^2` -
-
Question 4 of 6
4. Question
From the radial survey below, find `angleBOC`: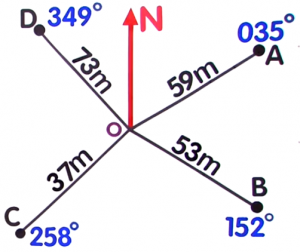
- `angleBOC=` (106)`°`
Hint
Help VideoCorrect
Good Job!
Incorrect
A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.Notice that `angleBOC` is the difference between the bearings of `B` and `C`.Subtract the bearing of `B` from the bearing of `C`.`angleBOC` `=` `angleC-angleB` `=` `258°-152°` Substitute the values `=` `106°`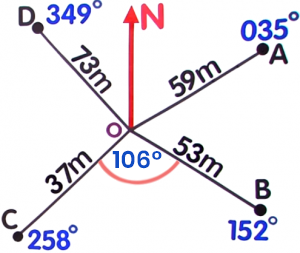 
`106°` -
Question 5 of 6
5. Question
From the radial survey below, find the area of `triangleBOC` to the nearest square metre.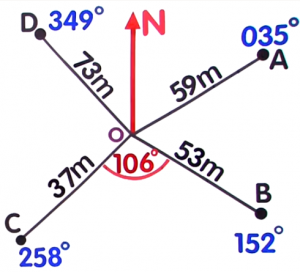
- Area of `triangleBOC=` (943)`m^2`
Hint
Help VideoCorrect
Great Work!
Incorrect
Area of a Non-Right Angled Triangle
`A_triangle=1/2``a``b``sin``C`where:
`a` is the side opposite angle `A`
`b` is the side opposite angle `B`
`c` is the side opposite angle `C`A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.First, identify the known values of the triangle `BOC`.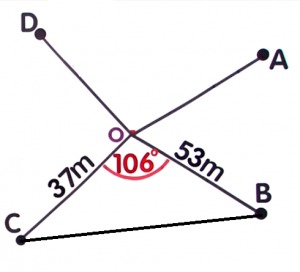
Now, substitute the known values to the formula and solve for the area.
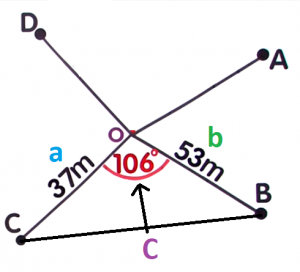`a=37m``b=53m``C=106°``A_triangle` `=` `1/2``a``b``sin``C` `=` `1/2(``37``)(``53``)sin``106°` Evaluate `sin` `106` on your calculator `=` `980.5times0.9612617°` Simplify `=` `942.517` `=` `943m^2` Round off to the nearest square metre `943m^2` -
Question 6 of 6
6. Question
From the radial survey below, find the length of `BC` to the nearest metre.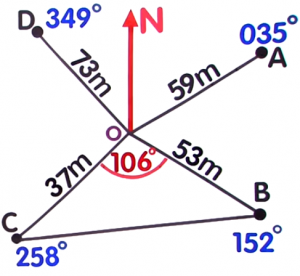
- `BC=` (73)`m`
Hint
Help VideoCorrect
Keep Going!
Incorrect
Cosine Law
$$\color{#007DDC}{a}^2=\color{#00880A}{b}^2+\color{#9a00c7}{c}^2-2\color{#00880A}{b}\color{#9a00c7}{c}\cos\color{#007DDC}{A}$$where:
`a` is the side opposite angle `A`
`b` is the side opposite angle `B`
`c` is the side opposite angle `C`Since `2` sides are given together with an angle between them, use the Cosine Law.First, label the triangle according to the Cosine Law.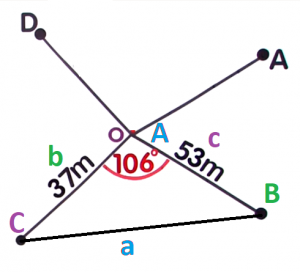
Substitute the three known values to the Cosine Law to find the length of side `BC` or `a`.From labelling the triangle, we know that the known values are those with labels `A, b` and `c`.`A=106°``b=37m``c=53m`$$\color{#007DDC}{a}^2$$ `=` $$\color{#00880A}{b}^2+\color{#9a00c7}{c}^2-2\color{#00880A}{b}\color{#9a00c7}{c}\cos\color{#007DDC}{A}$$ $$\color{#007DDC}{a}^2$$ `=` $$\color{#00880A}{37}^2+\color{#9a00c7}{53}^2-2(\color{#00880A}{37})(\color{#9a00c7}{53})\cos\color{#007DDC}{106°}$$ Evaluate `cos` `106` on your calculator `a^2` `=` `1369+2809-3922(-0.275637)` Simplify `a^2` `=` `4178+1081.0499` `a^2` `=` `5259.0499` `sqrt(a^2)` `=` `sqrt5259.0499` Take the square root of both sides `a` `=` `72.519m` `a` or `BC` `=` `73m` Round off to the nearest metre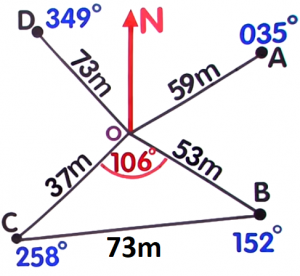 
`73m`