Volume of Shapes 1
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 7 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Answered
- Review
-
Question 1 of 7
1. Question
Find the volume of the Rectangular PrismThe given measurements are in units- `\text(Volume )=` (48) `\text(units)^3`
Hint
Help VideoCorrect
Great Work!
Incorrect
Volume of a Rectangular Prism
`\text(Volume )=``\text(side)``times``\text(side)``times``\text(depth)`In a regular cube, all sides are equalLabelling the given lengths
`\text(side)=4``\text(depth)=3`First, find the area of the front face`\text(Area)` `=` `\text(side)``times``\text(side)` Area of a Square `=` `4``times``4` Plug in the known lengths `=` `16 \text(units)^2` Next, multiply the area by the depth to find the volume`\text(Volume)` `=` `\text(area)``times``\text(depth)` Finding the volume `=` `16``times``3` Plug in the known lengths `=` `48 \text(units)^3` The given measurements are in units, so the volume is measured as units cubed`\text(Volume)=48 \text(units)^3` -
Question 2 of 7
2. Question
What is the volume of this cube?

- Volume`=` (729)`m^3`
Correct
Keep Going!
Incorrect
Volume of a Cube
`V=color(darkviolet)(s)^3`Labelling the given lengths
`color(darkviolet)(\text(side)=9)` Use the formula to find the volume
Use the formula to find the volume`V` `=` `color(darkviolet)(s)^3` Volume of a cube formula `=` `color(darkviolet)(9)^3` Plug in the known lengths `=` `729` Simplify `=` `729 \ m^3` The given measurements are in metres, so the volume is measured as metres cubedVolume`=729 \ m^3` -
Question 3 of 7
3. Question
Find the volume of the Prism- `\text(Volume )=` (696) `\text(cm)^3`
Hint
Help VideoCorrect
Excellent!
Incorrect
Volume of a Triangular Prism
`\text(Volume )=1/2 times``\text(base)``times``\text(height)``times``\text(depth)`Labelling the given lengths
`\text(base)=8``\text(height)=6``\text(depth)=29`First, find the area of the front face`\text(Area)` `=` `1/2 times``\text(base)``times``\text(height)` Area of a Triangle `=` `1/2 times``8``times``6` Plug in the known lengths `=` `24 \text(cm)^2` Next, multiply the area by the depth to find the volume`\text(Volume)` `=` `\text(area)``times``\text(depth)` Finding the volume `=` `24``times``29` Plug in the known lengths `=` `696 \text(cm)^3` The given measurements are in centimetres, so the volume is measured as centimetres cubed`\text(Volume)=696 \text(cm)^3` -
Question 4 of 7
4. Question
What is the volume of this Rectangular Prism?
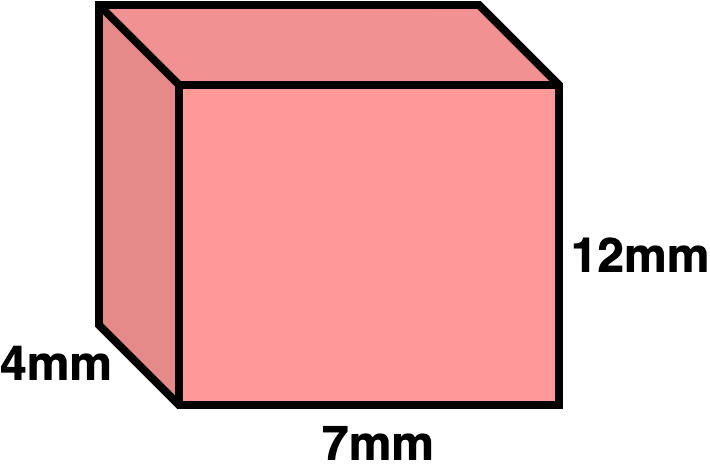
- Volume`=` (336)`mm^3`
Correct
Keep Going!
Incorrect
Volume of a Rectangular Prism
`V=color(royalblue)(\text(height)) xx color(darkviolet)(\text(width))xx color(green)(\text(depth))`Labelling the given lengths
`color(royalblue)(\text(height)=12)``color(darkviolet)(\text(width)=7)``color(green)(\text(depth)=4)` Use the formula to find the volume
Use the formula to find the volume`V` `=` `color(royalblue)(\text(height)) xx color(darkviolet)(\text(width))xx color(green)(\text(depth))` Volume of a Rectangular Prism formula `=` `color(royalblue)(\text(12)) xx color(darkviolet)(\text(7))xx color(green)(\text(4))` Plug in the known lengths `=` `336` `=` `336 \ mm^3` The given measurements are in millimetres, so the volume is measured as millimetres cubedVolume`=336 \ mm^3` -
Question 5 of 7
5. Question
What is the volume of this cube?

- Volume`=` (2,197)`cm^3`
Correct
Keep Going!
Incorrect
Volume of a Cube
`V=color(darkviolet)(s)^3`Labelling the given lengths
`color(darkviolet)(\text(side)=13)` Use the formula to find the volume
Use the formula to find the volume`V` `=` `color(darkviolet)(s)^3` Volume of a cube formula `=` `color(darkviolet)(13)^3` Plug in the known lengths `=` `2,197` Simplify `=` `2,197 \ cm^3` The given measurements are in centimetres, so the volume is measured as centimetres cubedVolume`=2,197 \ cm^3` -
Question 6 of 7
6. Question
Find the volume of the CylinderRound your answer to `2` decimal placesUse `pi=3.141592654`- `\text(Volume )=` (254.47, 254.34, 254.57) `\text(m)^3`
Hint
Help VideoCorrect
Nice Job!
Incorrect
Volume of a Cylinder
`\text(Volume)=pi times``\text(radius)^2``times``\text(height)`Labelling the given lengths
`\text(radius)=3``\text(height)=9`Use the formula to find the volumeUse `pi=3.141592654` See `pi` explained`\text(Volume)` `=` `pi times``\text(radius)^2``times``\text(height)` Volume of a Cylinder formula `=` `3.141592654 times``3^2``times``9` Plug in the known lengths `=` `3.141592654 times 9 times 9` Simplify `=` `254.46900` `=` `254.47 \text(m)^3` Rounded to `2` decimal places The given measurements are in metres, so the volume is measured as metres cubed`\text(Volume)=254.47 \text(m)^3`The answer will depend on which `pi` you use.In this solution we used: `pi=3.141592654`.Using Answer `pi=3.141592654` `254.47 m^3` `pi=3.14` `254.34 m^3` `pi=(22)/(7)` `254.57 m^3` -
Question 7 of 7
7. Question
Find the volume of the SphereRound your answer to `1` decimal placeUse `pi=3.141592654`- `\text(Volume )=` (57905.8, 57876.5, 57929.1) `\text(cm)^3`
Hint
Help VideoCorrect
Well Done!
Incorrect
Volume of a Sphere
`\text(Volume)=4/3 times pi times``\text(radius)^3`Labelling the given lengths
`\text(radius)=?``\text(diameter)=48`Recall that the radius is equal to half of the diameter`\text(radius)` `=` `1/2 times ``48` `\text(radius)` `=` `24` Now we can use the formula to find the volumeUse `pi=3.141592654` See `pi` explained`\text(Volume)` `=` `4/3 times pi times``\text(radius)^3` Volume of a Sphere formula `=` `4/3 times 3.141592654 times``24^3` Plug in the known lengths `=` `4/3 times 3.141592654 times 13824` Simplify `=` `57905.83579` `=` `57905.8 \text(cm)^3` Rounded to one decimal place The given measurements are in centimetres, so the volume is measured as centimetres cubed`\text(Volume)=57905.8 \text(cm)^3`The answer will depend on which `pi` you use.In this solution we used: `pi=3.141592654`.Using Answer `pi=3.141592654` `57905.8 cm^3` `pi=3.14` `57876.5 cm^3` `pi=(22)/(7)` `57929.1 cm^3`
Quizzes
- Volume of Shapes 1
- Volume of Shapes 2
- Volume of Shapes 3
- Volume of Shapes 4
- Volume of Composite Shapes 1
- Volume of Composite Shapes 2
- Surface Area of Shapes 1
- Surface Area of Shapes 2
- Surface Area of Shapes 3
- Surface Area and Volume Mixed Review 1
- Surface Area and Volume Mixed Review 2
- Surface Area and Volume Mixed Review 3
- Surface Area and Volume Mixed Review 4










