Years
>
Year 8>
Fractions>
Find the Fraction of a Quantity: Word Problems>
Find the Fraction of a Quantity: Word Problems 3Find the Fraction of a Quantity: Word Problems 3
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
Jack brings `$40` to the cinema. He spends `1/4` of that amount on one movie ticket and `3/5` on snacks. What is the remaining amount of money?- `$` (6)
Hint
Help VideoCorrect
Nice Job!
Incorrect
To multiply fractions, simply multiply the numerators and denominators separately.First, find the fraction for the money spent by adding the two given fractions.Fraction for snacks: `3/5`Fraction for ticket: `1/4`$$\frac{\color{#00880A}{3}}{\color{#9a00c7}{5}}+\frac{\color{#007DDC}{1}}{\color{#9a00c7}{4}}$$ `=` $$\frac{(\color{#00880A}{3}\times\color{#9a00c7}{4})+(\color{#007DDC}{1}\times\color{#9a00c7}{5})}{\color{#9a00c7}{5\times4}}$$ `=` `(12+5)/20` `=` `17/20` Proceed to compute for the actual money that Jack spentTo get a fraction of a quantity, simply multiply the fraction to the quantity.Fraction of money spent: `17/20`Total money: `$40``17/20``xx``40` `=` `17/20xx40/1` `=` $$\frac{17}{20\div\color{#CC0000}{20}}\times\frac{40\div\color{#CC0000}{20}}{1}$$ Reduce the fractions `=` `17/1xx2/1` `=` `34/1` `=` `$34` Jack spent $34 in the cinema.Finally, subtract the money spent from the total money to get the remaining amount.`$40-$34` `=` `$6` There is `$6` left from Jack’s money.`$6` -
Question 2 of 5
2. Question
A petrol tank has a capacity of `60L`. It is currently `1/3` full. How many more litres need to be added before the tank becomes full?- (40)`L`
Hint
Help VideoCorrect
Excellent!
Incorrect
To multiply fractions, simply multiply the numerators and denominators separately.First, compute for the exact amount of fuel in the tank at the momentTo get a fraction of a quantity, simply multiply the fraction to the quantity.Fraction of current fuel amount: `1/3`Total tank capacity: `60L``1/3``xx``60` `=` `1/3xx60/1` `=` $$\frac{1}{3\div\color{#CC0000}{3}}\times\frac{60\div\color{#CC0000}{3}}{1}$$ Reduce the fractions `=` `1/1xx20/1` `=` `20/1` `=` `20L` The tank currently contains `20L` of petrol.Finally, subtract the current amount of petrol from the total capacity to get how much petrol needs to be added.`60L-20L` `=` `40L` `40L` of petrol needs to be added for the tank to be full.`40L` -
Question 3 of 5
3. Question
A `1` metre pole is placed in a pond. `1/5` of it is in the ground and `2/3` of it is in the water. What fraction of the pole is above the water?Write fractions in the format “a/b”- (2/15)
Hint
Help VideoCorrect
Keep Going!
Incorrect
Subtract the given fractions from the full length of the pole.Length of the pole: `1`mLength of pole in water: `2/3`Length of pole in the ground: `1/5``1-(\frac{\color{#00880A}{2}}{\color{#9a00c7}{3}}+\frac{\color{#007DDC}{1}}{\color{#9a00c7}{5}})` `=` $$1-\frac{(\color{#00880A}{2}\times\color{#9a00c7}{5})+(\color{#007DDC}{1}\times\color{#9a00c7}{3})}{\color{#9a00c7}{3\times5}}$$ Use cross method to add the fractions `=` $$1-\frac{10+3}{15}$$ `=` $$\frac{15}{15}-\frac{13}{15}$$ `=` $$\frac{2}{15}$$ `2/15` of the pole is above water.`2/15` -
Question 4 of 5
4. Question
From a squad of `15` players, `1/3` are injured. How many are not injured?- (10) players
Hint
Help VideoCorrect
Correct!
Incorrect
To multiply fractions, simply multiply the numerators and denominators separately.First, get the fraction of players that are not injured.Total squad of players: `3/3`Fraction of injured players: `1/3``3/3-1/3` `=` `2/3` `2/3` of the players are not injured.To get a fraction of a quantity, simply multiply the fraction to the quantity.Fraction of injured players: `2/3`Total no. of players: `15``2/3``xx``15` `=` `2/3xx15/1` `=` $$\frac{2}{3\div\color{#CC0000}{3}}\times\frac{15\div\color{#CC0000}{3}}{1}$$ Reduce the fractions `=` `2/1xx5/1` `=` `10/1` `=` `10` players `10` players in the squad are not injured.`10` players -
Question 5 of 5
5. Question
Jason buys eight `500`g cans of dog food. Eventually, `1 1/5`kg worth is eaten. How much dog food remains?Hint
Help VideoCorrect
Well Done!
Incorrect
To multiply fractions, simply multiply the numerators and denominators separately.Transforming a Fraction from Mixed to Improper
`=` $$\frac{(\color{#9a00c7}{c}\times\color{#00880A}{a})+\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ Transforming an Improper to Mixed Fraction
$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}=\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$`(``b``-:``c``)=``Q` and `R` is the remainderTo get a fraction of a quantity, simply multiply the fraction to the quantity.`1` can of dog food: `500`g or `1/2`kgNo. of cans: `8`kg`1/2``xx``8` `=` `1/2xx8/1` `=` `8/2` `=` `8-:2` `=` `4`kg Jason bought `4`kg of dog food in totalSubtract the amount of eaten dog food from the total amount of dog food.Total amount: `4`kgAmount eaten: `1 1/5`kg$$4-\color{#00880A}{1}\frac{\color{#007DDC}{1}}{\color{#9a00c7}{5}}$$ Convert the fraction from mixed to improper `=` $$4-\frac{(\color{#9a00c7}{5}\times\color{#00880A}{1})+\color{#007DDC}{1}}{\color{#9a00c7}{5}}$$ `=` $$4-\frac{5+1}{5}$$ `=` $$4-\frac{6}{5}$$ `=` $$\frac{20}{5}-\frac{6}{5}$$ Reduce the fractions `=` `14/5` Convert the fraction from improper to mixed by dividing the numerator by the denominatorArrange the numbers for long division `5` goes into `14` once. So write `2` above the line.
`5` goes into `14` once. So write `2` above the line.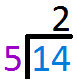 Multiply `2` to `5` and write the answer below `14`
Multiply `2` to `5` and write the answer below `14`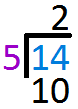 Subtract `10` from `14` and write the answer one line below
Subtract `10` from `14` and write the answer one line below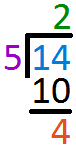 Since `5` cannot go into `4` anymore, `4` is left as the Remainder and `2` is the QuotientSubstitute values into the given formula
Since `5` cannot go into `4` anymore, `4` is left as the Remainder and `2` is the QuotientSubstitute values into the given formula$$\frac{\color{#007DDC}{b}}{\color{#9a00c7}{c}}$$ `=` $$\color{#00880A}{Q}\frac{\color{#e65021}{R}}{\color{#9a00c7}{c}}$$ $$\frac{\color{#007DDC}{14}}{\color{#9a00c7}{5}}$$ `=` $$\color{#00880A}{2}\frac{\color{#e65021}{4}}{\color{#9a00c7}{5}}$$ `2 4/5`kg of dog food remains.`2 4/5`kg
Quizzes
- Shaded Fractions 1
- Shaded Fractions 2
- Equivalent Fractions 1
- Equivalent Fractions 2
- Equivalent Fractions 3
- Equivalent Fractions 4
- Simplify Fractions 1
- Simplify Fractions 2
- Simplify Fractions 3
- Find the Lowest Common Denominator
- Comparing Fractions 1
- Comparing Fractions 2
- Comparing Fractions 3
- Mixed and Improper Fractions 1
- Mixed and Improper Fractions 2
- Mixed and Improper Fractions 3
- Add and Subtract Fractions 1
- Add and Subtract Fractions 2
- Add and Subtract Fractions 3
- Add and Subtract Fractions 4
- Multiply and Divide Fractions 1
- Multiply and Divide Fractions 2
- Multiply and Divide Fractions 3
- Add and Subtract Mixed Numbers 1
- Add and Subtract Mixed Numbers 2
- Add and Subtract Mixed Numbers 3
- Multiply and Divide Mixed Numbers 1
- Multiply and Divide Mixed Numbers 2
- Multiply and Divide Mixed Numbers 3
- Multiply and Divide Mixed Numbers 4
- Fraction Word Problems: Addition and Subtraction 1
- Fraction Word Problems: Addition and Subtraction 2
- Fraction Word Problems: Addition and Subtraction 3
- Fraction Word Problems: Addition and Subtraction 4
- Fraction Word Problems: Multiplication and Division
- Find the Fraction of a Quantity
- Find the Quantity of a Quantity 1
- Find the Quantity of a Quantity 2
- Find the Fraction of a Quantity: Word Problems 1
- Find the Fraction of a Quantity: Word Problems 2
- Find the Fraction of a Quantity: Word Problems 3
- Find the Fraction of a Quantity: Word Problems 4
- Find the Quantity of a Quantity: Word Problems
- Order of Operations Involving Fractions 1
- Order of Operations Involving Fractions 2




