Division of Polynomials

Years

Try VividMath Premium to unlock full access

Start Free Trial

Lets see your results!

Points

Score

Time

Retry Quiz

Answered
Review

Question 1 of 5

Solve

(x^{2} + 12 x + 7) \div 6 x

$(x^2+12x+7)divide6x$

1. $x^{2} + 9$ $x^2+9$
2. $x + 2 + \frac{7}{6 x}$ $x+2+7/(6x)$
3. $\frac{x}{6} + 3$ $x/6+3$
4. $\frac{x}{6} + 2 + \frac{7}{6 x}$ $x/6+2+7/(6x)$

Question 2 of 5

2. Question
Solve

$(x^{2} + 5 x - 7) \div (x - 2)$ $(x^2+5x-7)divide(x-2)$
- 1. $\frac{x + 7}{x - 2}$ $(x+7)/(x-2)$
- 2. $7 x + \frac{7}{x - 2}$ $7x+7/(x-2)$
- 3. $x + 7 + \frac{7}{x - 2}$ $x+7+7/(x-2)$
- 4. $\frac{7}{x - 2}$ $7/(x-2)$
Hint

Help Video
Correct

Correct!
Incorrect
Need Text
Play
Current Time 0:00
/
Duration Time 0:00
Remaining Time -0:00
Stream TypeLIVE
Loaded: 0%
Progress: 0%
0:00
Fullscreen
Video Acceleration:
On
Off

00:00
Mute
Playback Rate
1x
2x
1.5x
1.25x
1x
0.75x
0.5x
Subtitles
subtitles off
Captions
captions off
English
Chapters
Chapters

Division of Polynomials

$\mathsf{\frac{P}{Divisor}=Quotient+\frac{R}{Divisor}}$

where $\mathsf{P}$ is the Polynomial and $\mathsf{R}$ is the Remainder

Long Division

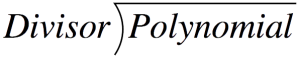Use long division when a polynomial is divided by a binomial

First, substitute components into the Long Division formula

$\mathsf{P}$ (Polynomial) $=$ $x^2+5x-7$

$\mathsf{Divisor}$ $=$ $x-2$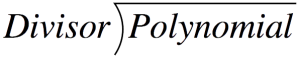

$=$

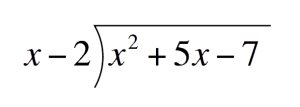Next, solve for each term of the quotient

First term of the quotient:

Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial

$x^2dividex$ $=$ $x$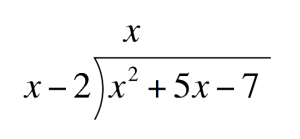

Multiply $x$ to the divisor. Place this under the Polynomial

$x$ $(x-2)$ $=$ $x^2-2x$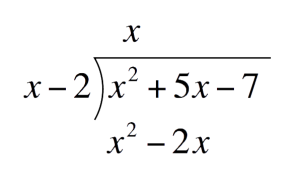

Subtract $x^2-2x$ and write the difference one line below

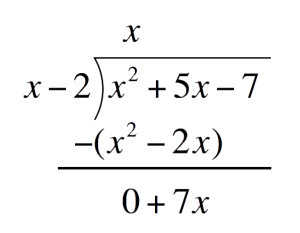Drop down $-7$ and repeat the process to get the second term of the quotient

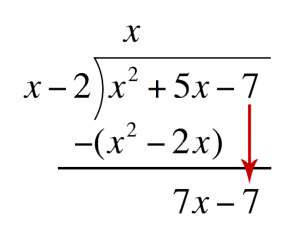Second term of the quotient:

Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial

$7xdividex$ $=$ $7$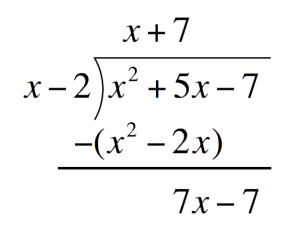

Multiply $7$ to the divisor. Place this one line below

$7$ $(x-2)$ $=$ $7x-14$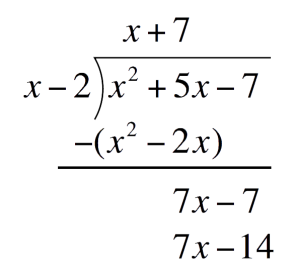

Subtract $7x-14$ and write the difference one line below

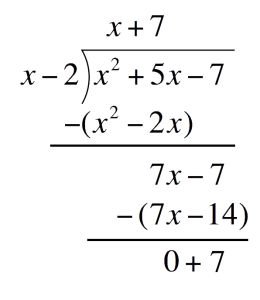Since $7$ is not divisible by the divisor ( $x-2$ ) anymore, it is left as the Remainder

This also means that the expression at the very top is the Quotient

Finally, combine and substitute the components into the Division of Polynomials formula

$\mathsf{P}$ (Polynomial) $=$ $x^2+5x-7$

$\mathsf{Divisor}$ $=$ $x-2$

$\mathsf{Quotient}$ $=$ $x+7$

$\mathsf{Remainder}$ $=$ $7$

$\mathsf{\frac{P}{Divisor}}$ $=$ $\mathsf{Quotient+\frac{R}{Divisor}}$ Division of Polynomials

$\frac{x^2+5x-7}{x-2}$ $=$ $x+7+\frac{7}{x-2}$ Substitute

$x+7+7/(x-2)$

Question 3 of 5

Solve

$(2x^3+x^2+4x+1)/(x-3)$

1. $x^2+7x+76/(x-3)$
2. $2x^2+7x+25+76/(x-3)$
3. $7x+25+75/(x-3)$
4. $2x^2+7x+20+101/(x-3)$

Incorrect

Need Text

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

$\mathsf{\frac{P}{Divisor}=Quotient+\frac{R}{Divisor}}$

where

$\mathsf{P}$ is the Polynomial and

$\mathsf{R}$ is the Remainder

Long Division

Use long division when a polynomial is divided by a binomial

First, substitute components into the Long Division formula

$\mathsf{P}$ (Polynomial)	$=$	$2x^3+x^2+4x+1$
$\mathsf{Divisor}$	$=$	$x-3$

$=$

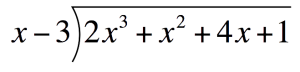Next, solve for each term of the quotient

First term of the quotient:

Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial

$2x^3dividex$

$=$

$2x^2$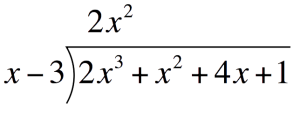

Multiply $2x^2$ to the divisor. Place this under the Polynomial

$2x^2$

$(x-3)$

$=$

$2x^3-6x^2$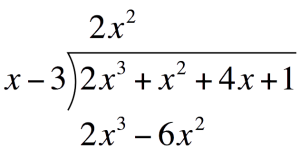

Subtract $2x^3-6x^2$ and write the difference one line below

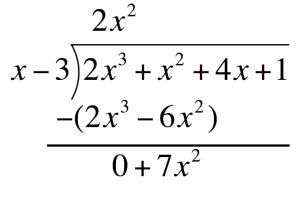Drop down

$4x$ and repeat the process to get the second term of the quotient

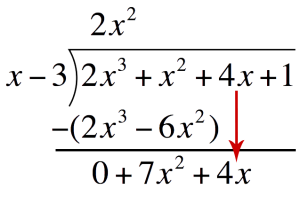Second term of the quotient:

Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial

$7x^2dividex$

$=$

$7x$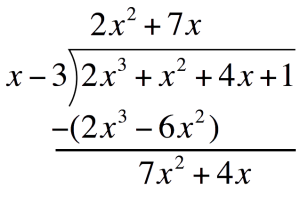

Multiply $7x$ to the divisor. Place this one line below

$7x$

$(x-3)$

$=$

$7x^2-21x$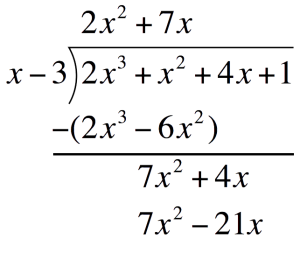

Subtract $7x^2-21x$ and write the difference one line below

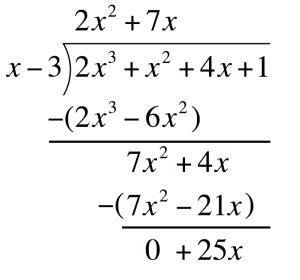Drop down

$1$ and repeat the process to get the second term of the quotient

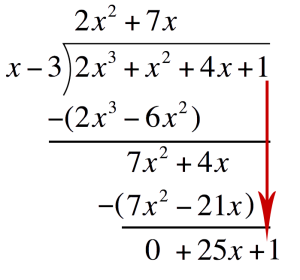Third term of the quotient:

Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial

$25xdividex$

$=$

$25$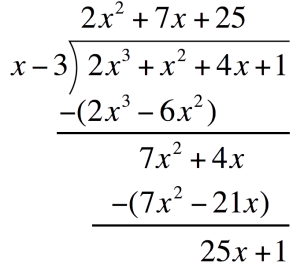

Multiply $25$ to the divisor. Place this one line below

$25$

$(x-3)$

$=$

$25x-75$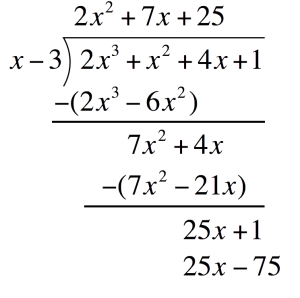

Subtract $25x-75$ and write the difference one line below

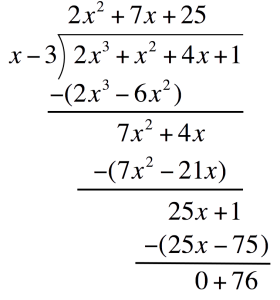Since

$76$ is not divisible by the divisor (

$x-3$ ) anymore, it is left as the Remainder

This also means that the expression at the very top is the Quotient

Finally, combine and substitute the components into the Division of Polynomials formula

$\mathsf{P}$ (Polynomial)	$=$	$2x^3+x^2+4x+1$
$\mathsf{Divisor}$	$=$	$x-3$
$\mathsf{Quotient}$	$=$	$2x^2+7x+25$
$\mathsf{Remainder}$	$=$	$76$

$\mathsf{\frac{P}{Divisor}}$	$=$	$\mathsf{Quotient+\frac{R}{Divisor}}$	Division of Polynomials

$\frac{2x^3+x^2+4x+1}{x-3}$	$=$	$2x^2+7x+25+\frac{76}{x-3}$	Substitute

$2x^2+7x+25+76/(x-3)$

Question 4 of 5

4. Question
Solve and give your answer in the format $\mathsf{P=Divisor\times{Quotient}+R}$

$(8-y^2)divide(y-3)$
- 1. $-y-3+1/(y-3)$
- 2. $(y-3)(-y-3)-1$
- 3. $(-y-3)^2+1$
- 4. $y-2+5/(y-3)$
Hint

Help Video
Correct

Fantastic!
Incorrect
Need Text
Play
Current Time 0:00
/
Duration Time 0:00
Remaining Time -0:00
Stream TypeLIVE
Loaded: 0%
Progress: 0%
0:00
Fullscreen
Video Acceleration:
On
Off

00:00
Mute
Playback Rate
1x
2x
1.5x
1.25x
1x
0.75x
0.5x
Subtitles
subtitles off
Captions
captions off
English
Chapters
Chapters

Division of Polynomials

$\mathsf{P=Divisor\times{Quotient}+R}$

where $\mathsf{P}$ is the Polynomial and $\mathsf{R}$ is the Remainder

Long Division

Use long division when a polynomial is divided by a binomial

First, notice that the $y$ -term with the power of 1 is missing. Add this term to the polynomial and arrange the terms in descending powers before using long division

$\mathsf{P}$ (Polynomial) $=$ $8-y^2$

$=$ $-y^2+$ $0y$ $+8$

$\mathsf{Divisor}$ $=$ $y-3$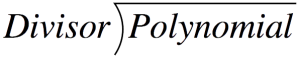

$=$

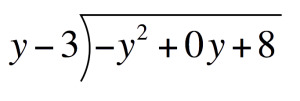Next, solve for each term of the quotient

First term of the quotient:

Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial

$-y^2dividey$ $=$ $-y$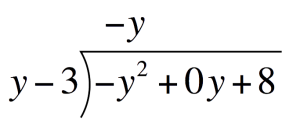

Multiply $-y$ to the divisor. Place this under the Polynomial

$-y$ $(y-3)$ $=$ $-y^2+3y$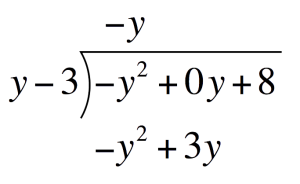

Subtract $-y^2+3y$ and write the difference one line below

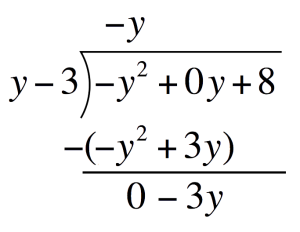Drop down $8$ and repeat the process to get the second term of the quotient

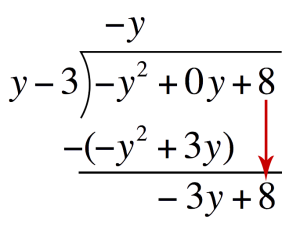Second term of the quotient:

Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial

$-3ydividey$ $=$ $-3$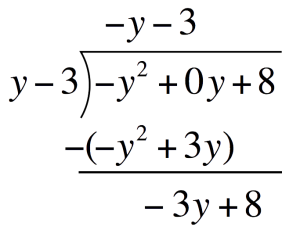

Multiply $-3$ to the divisor. Place this one line below

$-3$ $(y-3)$ $=$ $-3y+9$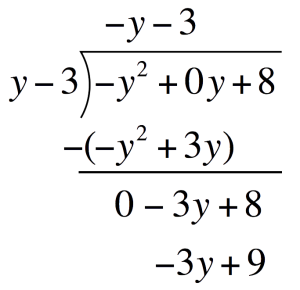

Subtract $-3y+9$ and write the difference one line below

Since $-1$ is not divisible by the divisor ( $y-3$ ) anymore, it is left as the Remainder

This also means that the expression at the very top is the Quotient

Finally, combine and substitute the components into the Division of Polynomials formula

$\mathsf{P}$ (Polynomial) $=$ $8-y^2$

$\mathsf{Divisor}$ $=$ $y-3$

$\mathsf{Quotient}$ $=$ $-y-3$

$\mathsf{Remainder}$ $=$ $-1$

$\mathsf{P}$ $=$ $\mathsf{Divisor\times{Quotient}+R}$ Division of Polynomials

$=$ $(y-3)(-y-3)-1$ Substitute

$(y-3)(-y-3)-1$

Question 5 of 5

Solve

$(x^4-x^3-17x^2-13x+1)/(x^2+2x)$

1. $2x^2-3x-1+(9x-1)/(x^2+2x)$
2. $x^2+x-12+(3x-1)/(x^2+2x)$
3. $x^2-5x+(9x)/(x^2+2x)$
4. $x^2-3x-11+(9x+1)/(x^2+2x)$

Incorrect

Need Text

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

Division of Polynomials

$\mathsf{\frac{P}{Divisor}=Quotient+\frac{R}{Divisor}}$

where

$\mathsf{P}$ is the Polynomial and

$\mathsf{R}$ is the Remainder

Long Division

Use long division when a polynomial is divided by a binomial

First, substitute components into the Long Division formula

$\mathsf{P}$ (Polynomial)	$=$	$x^4-x^3-17x^2-13x+1$
$\mathsf{Divisor}$	$=$	$x^2+2x$

$=$

Next, solve for each term of the quotient

First term of the quotient:

Divide the first term of the Polynomial by the first term of the Divisor. Place this above the Polynomial

$x^4dividex^2$

$=$

$x^2$

Multiply $x^2$ to the divisor. Place this under the Polynomial

$x^2$

$(x^2+2x)$

$=$

$x^4+2x^3$

Subtract $x^4+2x^3$ and write the difference one line below

Drop down

$-17x^2$ and repeat the process to get the second term of the quotient

Second term of the quotient:

Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial

$-3x^3dividex^2$

$=$

$-3x$

Multiply $-3x$ to the divisor. Place this one line below

$-3x$

$(x^2+2x)$

$=$

$-3x^3-6x^2$

Subtract $-3x^3-6x^2$ and write the difference one line below

Drop down

$-13x$ and repeat the process to get the third term of the quotient

Third term of the quotient:

Divide the first term of the bottom expression by the first term of the Divisor. Place this above the Polynomial

$-11x^2dividex^2$

$=$

$-11$

Multiply $-11$ to the divisor. Place this one line below

$-11$

$(x^2+2x)$

$=$

$-11x^2-22x$

Subtract $-11x^2-22x$ and write the difference one line below

Drop down

$1$ to see if a fourth term can be added to the quotient

Since

$9x+1$ is not divisible by the divisor (

$x^2+2x$ ) anymore, it is left as the Remainder

This also means that the expression at the very top is the Quotient

Finally, combine and substitute the components into the Division of Polynomials formula

$\mathsf{P}$ (Polynomial)	$=$	$x^4-x^3-17x^2-13x+1$
$\mathsf{Divisor}$	$=$	$x^2+2x$
$\mathsf{Quotient}$	$=$	$x^2-3x-11$
$\mathsf{Remainder}$	$=$	$9x+1$

$\mathsf{\frac{P}{Divisor}}$	$=$	$\mathsf{Quotient+\frac{R}{Divisor}}$	Division of Polynomials

$\frac{x^4-x^3-17x^2-13x+1}{x^2+2x}$	$=$	$x^2-3x-11+\frac{9x+1}{x^2+2x}$	Substitute

$x^2-3x-11+(9x+1)/(x^2+2x)$

$(x^{2} + 12 x + 7) \div 6 x$ $(x^2+12x+7)divide6x$	$=$ $=$	$\frac{x^{2} + 12 x + 7}{6 x}$ $(x^2+12x+7)/(6x)$

	$=$ $=$	$\frac{x^{2}}{6 x} + \frac{12 x}{6 x} + \frac{7}{6 x}$ $(x^2)/(6x)+(12x)/(6x)+7/(6x)$	Separate terms

	$=$ $=$	$\frac{x}{6} + 2 + \frac{7}{6 x}$ $x/6+2+7/(6x)$	Simplify

Division of Polynomials

Try VividMath Premium to unlock full access

Quiz summary

Information

1. Question

Hint

Great Work!

2. Question

Hint

Correct!

Division of Polynomials

Long Division

3. Question

Hint

Keep Going!

Division of Polynomials

Long Division

4. Question

Hint

Fantastic!

Division of Polynomials

Long Division

5. Question

Hint

Excellent!

Division of Polynomials

Long Division

Quizzes

$\mathsf{P}$ (Polynomial)	$=$	$x^2+5x-7$
$\mathsf{Divisor}$	$=$	$x-2$

$\mathsf{P}$ (Polynomial)	$=$	$8-y^2$
	$=$	$-y^2+$ $0y$ $+8$
$\mathsf{Divisor}$	$=$	$y-3$

$\mathsf{P}$	$=$	$\mathsf{Divisor\times{Quotient}+R}$	Division of Polynomials

	$=$	$(y-3)(-y-3)-1$	Substitute