Add and Subtract Surd Expressions 1
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
Simplify
`sqrt18+sqrt32-2sqrt2`
Correct
Great Work!
Incorrect
A radicand is the number under the square root symbol.
Terms with the same radicand are like terms. We can evaluate the coefficients of like terms.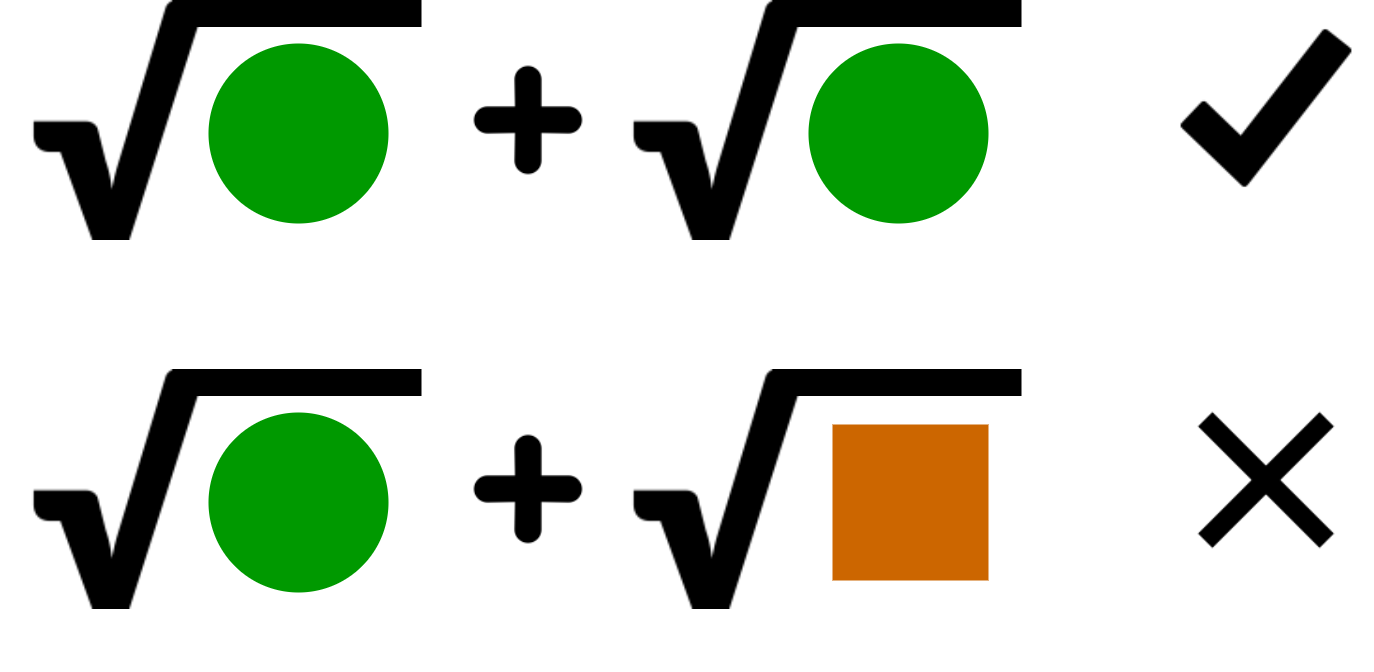
Evaluate the coefficients of like terms (same radicand).`=` `sqrt18+sqrt32-2sqrt2` Find two multiples of 18 and for 32 where one is a perfect square. `=` `sqrt9 xx sqrt2 + sqrt16 xx sqrt2-2sqrt2` Simplify `=` `color(royalblue)(3)color(forestgreen)(sqrt2)+color(royalblue)(4)color(forestgreen)(sqrt2)-color(royalblue)(2)color(forestgreen)(sqrt2)` `=` `color(royalblue)((3+4-2))color(forestgreen)(sqrt2)` Evaluate `=` `5sqrt2` `5sqrt2` -
Question 2 of 5
2. Question
Simplify
`sqrt98+2sqrt50`
Correct
Great Work!
Incorrect
A radicand is the number under the square root symbol.
Terms with the same radicand are like terms. We can evaluate the coefficients of like terms.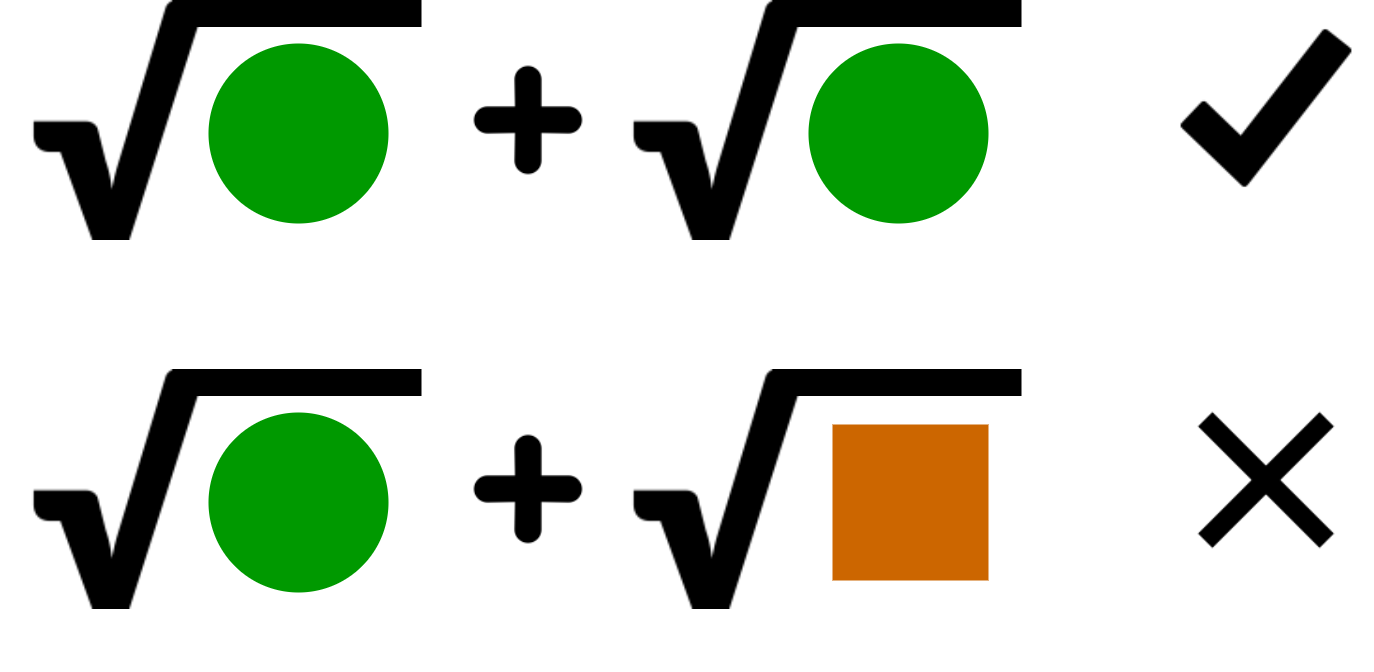Evaluate the coefficients of like terms (same radicand).`=` `sqrt98+2 xx sqrt50` Find two multiples of 98 and for 50 each where one is a perfect square. `=` `sqrt49 xx sqrt2+2 xx sqrt25 xx sqrt2` Simplify `=` `7 xx sqrt2+2 xx 5 xx sqrt2` `49` and `25` are perfect squares `=` `color(royalblue)(7)color(forestgreen)(sqrt2)+color(royalblue)(10)color(forestgreen)(sqrt2)` `=` `color(royalblue)(7+10)color(forestgreen)(sqrt2)` Evaluate coefficients `=` `17sqrt2` `17sqrt2` -
Question 3 of 5
3. Question
Simplify
`3sqrt75-2sqrt48`
Correct
Great Work!
Incorrect
A radicand is the number under the square root symbol.
Terms with the same radicand are like terms. We can evaluate the coefficients of like terms.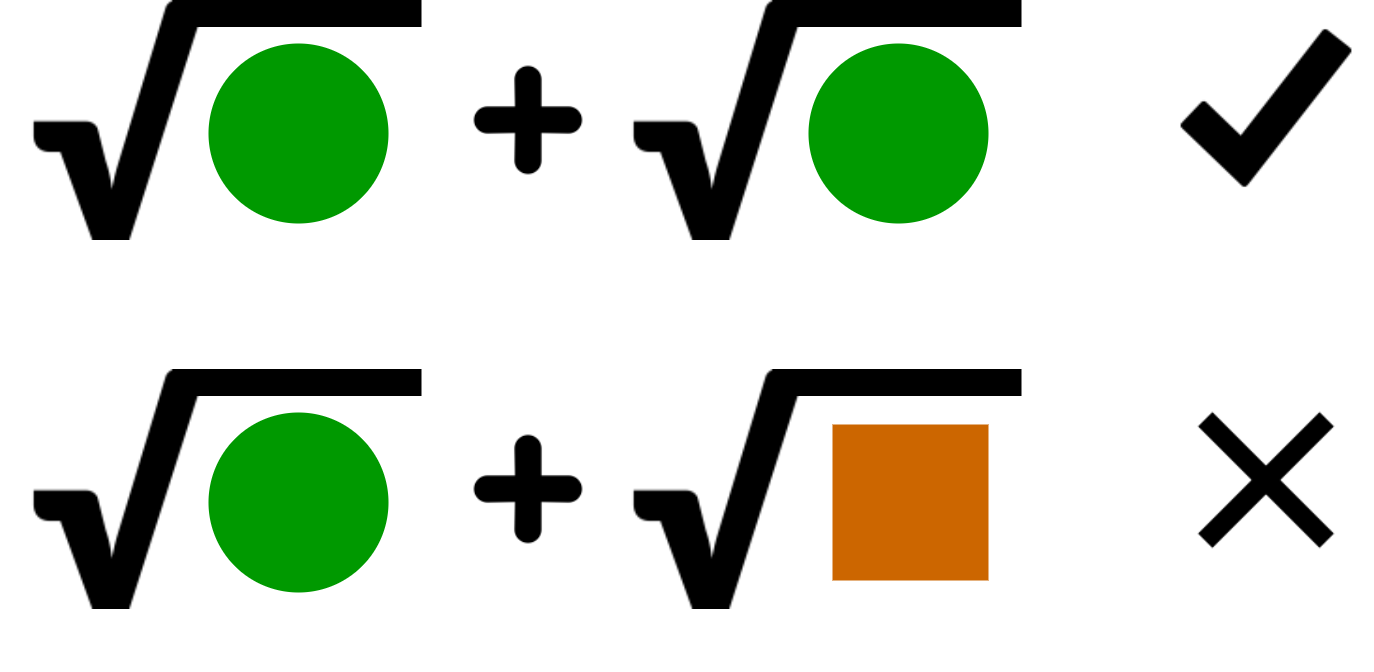Evaluate the coefficients of like terms (same radicand).`=` `3sqrt75-2sqrt48` Find two multiples of 75 and 48 each where one is a perfect square. `=` `3sqrt25 xx sqrt3-2sqrt16 xx sqrt3` Simplify `=` `3 xx 5sqrt3-2 xx 4sqrt3` `=` `color(royalblue)(15)color(forestgreen)(sqrt3)-color(royalblue)(8)color(forestgreen)(sqrt3)` `=` `color(royalblue)(15-8)color(forestgreen)(sqrt3)` Evaluate coefficients `=` `7sqrt3` `7sqrt3` -
Question 4 of 5
4. Question
Simplify
`2sqrt48+sqrt27-4sqrt3`
Correct
Great Work!
Incorrect
A radicand is the number under the square root symbol.
Terms with the same radicand are like terms. We can evaluate the coefficients of like terms.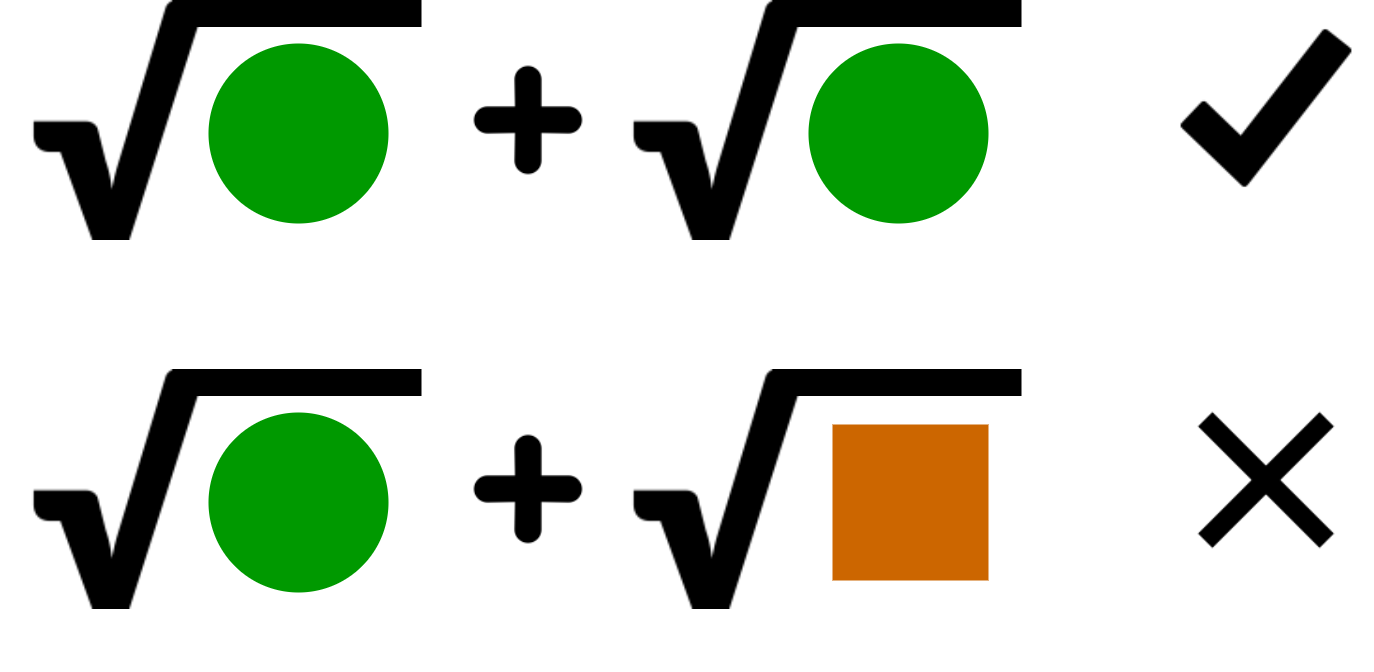Evaluate the coefficients of like terms (same radicand).`=` `2sqrt48+sqrt27-4sqrt3` Find two multiples of 48 and 27 each where one is a perfect square. `=` `2sqrt16 xx sqrt3+sqrt9 xx sqrt3-4sqrt3` Simplify `=` `2 xx 4sqrt3+3sqrt3-4sqrt3` `16` and `9` are perfect squares `=` `color(royalblue)(8)color(forestgreen)(sqrt3)+color(royalblue)(3)color(forestgreen)(sqrt3)-color(royalblue)(4)color(forestgreen)(sqrt3)` `=` `color(royalblue)(8+3-4)color(forestgreen)(sqrt3)` Evaluate coefficients `=` `7sqrt3` `7sqrt3` -
Question 5 of 5
5. Question
Simplify
`7sqrt3+sqrt50-sqrt12`
Correct
Great Work!
Incorrect
A radicand is the number under the square root symbol.
Terms with the same radicand are like terms. We can evaluate the coefficients of like terms.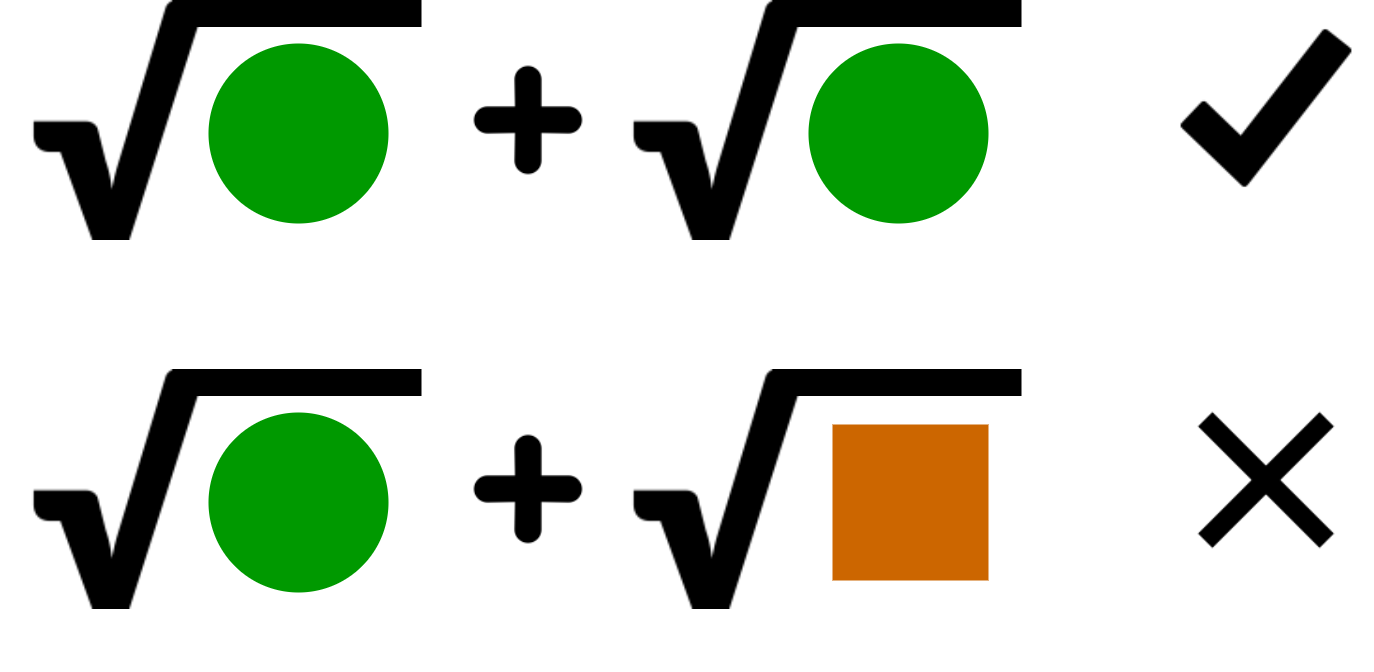Evaluate the coefficients of like terms (same radicand).`=` `7sqrt3+sqrt50-sqrt12` Find two multiples of 50 and 12 each where one is a perfect square. `=` `7sqrt3+sqrt25 xx sqrt2-sqrt4 xx sqrt3` Simplify `=` `7sqrt3+5sqrt2-2sqrt3` `25` and `4` are perfect squares `=` `color(royalblue)(7)color(forestgreen)(sqrt3)+5sqrt2-color(royalblue)(2)color(forestgreen)(sqrt3)` `=` `color(royalblue)(7-2)color(forestgreen)(sqrt3)+5sqrt2` Evaluate coefficients `=` `5sqrt3+5sqrt2` `5sqrt3+5sqrt2`
Quizzes
- Simplify Square Roots 1
- Simplify Square Roots 2
- Simplify Square Roots 3
- Simplify Square Roots 4
- Simplify Surds with Variables 1
- Simplify Surds with Variables 2
- Simplify Surds with Variables 3
- Rewriting Entire and Mixed Surds 1
- Rewriting Entire and Mixed Surds 2
- Add and Subtract Surd Expressions (Basic) 1
- Add and Subtract Surd Expressions (Basic) 2
- Add and Subtract Surd Expressions (Basic) 3
- Add and Subtract Surd Expressions 1
- Add and Subtract Surd Expressions 2
- Add and Subtract Surd Expressions 3
- Multiply Surd Expressions 1
- Multiply Surd Expressions 2
- Multiply Surd Expressions 3
- Multiply Surd Expressions 4
- Divide Surd Expressions 1
- Divide Surd Expressions 2
- Divide Surd Expressions 3
- Multiply and Divide Surd Expressions
- Simplify Surd Expressions using the Distributive Property 1
- Simplify Surd Expressions using the Distributive Property 2
- Simplify Surd Expressions using the Distributive Property 3
- Simplify Binomial Surd Expressions using the FOIL Method 1
- Simplify Binomial Surd Expressions using the FOIL Method 2
- Rationalising the Denominator 1
- Rationalising the Denominator 2
- Rationalising the Denominator 3
- Rationalising the Denominator 4
- Rationalising the Denominator using Conjugates