Years
>
Year 12>
Simultaneous Equations>
Solve Simultaneous Equations by Graphing>
Solve Simultaneous Equations by GraphingSolve Simultaneous Equations by Graphing
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 7 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Answered
- Review
-
Question 1 of 7
1. Question
Find the solution to the simultaneous equations by graphing.
`x-3=0`
`x+y=1`
- `x=` (3) `y=` (-2)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `x-3=0`Make `x` the subject to get the equation of the line.`x-3 \ color(crimson)(+3)` `=` `0 \ color(crimson)(+3)` Add `3` to both sides `x \ cancel(-3) cancel(+3)` `=` `0 \ color(crimson)(+3)` `x` `=` `3` 
Graph: `x+y=1`First, make `y` the subject.`x+y` `=` `1` `y` `=` `-x+1` Make `y` the subject Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `1` `0` `-1` `-2` Plot the points and draw the graph.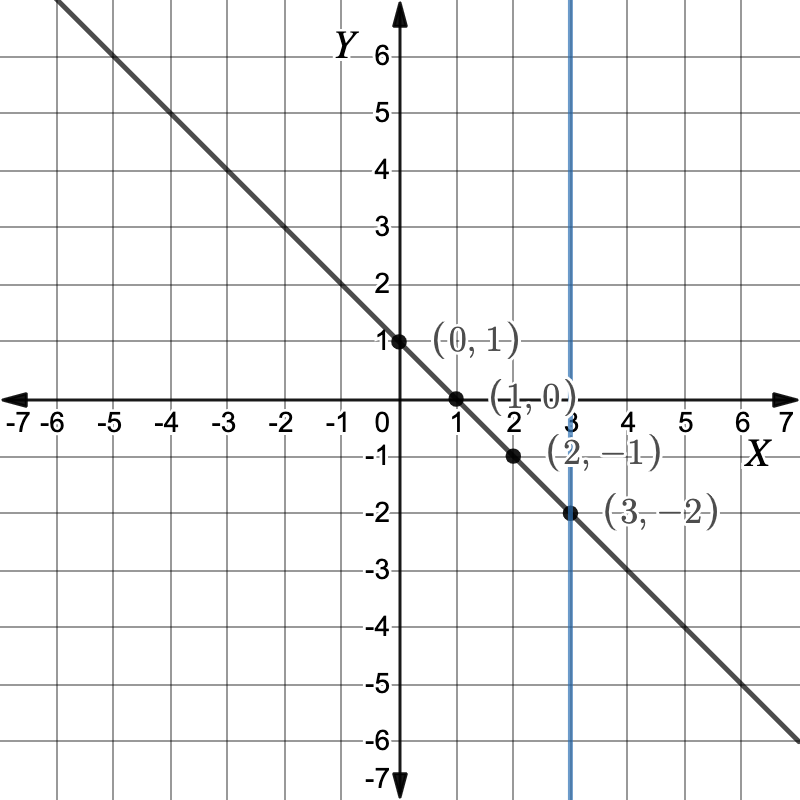
The graphs intersect at the point `(3,-2)`
`:. color(darkviolet)(x=3, \ y=-2)``x=3, y=-2` -
Question 2 of 7
2. Question
Find the solution to the simultaneous equations by graphing.
`2x+y=5`
`5x-3y=7`
- `x=` (2) `y=` (1)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `2x+y=5`Make `y` the subject to get the equation of the line.`2x+y \ color(crimson)(-2x)` `=` `5 \ color(crimson)(-2x)` Add `-2x` to both sides `y \ cancel(+2x) cancel(-2x)` `=` `5 \ color(crimson)(-2x)` `y` `=` `-2x+5` Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `5` `3` `1` `-1` Plot the points and draw the graph.
Graph: `5x-3y=7`First, make `y` the subject.`5x-3y` `=` `7` Make `y` the subject `-3y` `=` `-5x+7` Add `-5x` to both sides `y` `=` `5/3x-7/3` Divide both sides by `-3` Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `-7/3` `-2/3` `1` `8/3` Plot the points and draw the graph.
The graphs intersect at the point `(2,1)`
`:. color(darkviolet)(x=2, \ y=1)``x=2, y=1` -
Question 3 of 7
3. Question
Find the solution to the simultaneous equations by graphing.
`4x-3y=1`
`3x+2y=5`
- `x=` (1) `y=` (1)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `4x-3y=1`Make `y` the subject to get the equation of the line.`4x-3y \ color(crimson)(-4x)` `=` `1 \ color(crimson)(-4x)` Add `-4x` to both sides `-3y \ cancel(+4x) cancel(-4x)` `=` `1 \ color(crimson)(-4x)` `\ color(crimson)(-3)y \ color(crimson)(\div(-3))` `=` `(-4x+1 )\ color(crimson)(\div(-3))` Divide both sides by `-3` `y` `=` `4/3x-1/3` Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `-1/3` `1` `7/3` `11/3` Plot the points and draw the graph.
Graph: `3x+2y=5`First, make `y` the subject.`3x+2y` `=` `5` Make `y` the subject `2y` `=` `-3x+5` Add `-3x` to both sides `y` `=` `-3/2x+5/2` Divide both sides by `2` Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `5/2` `1` `-1/2` `-2` Plot the points and draw the graph.
The graphs intersect at the point `(1,1)`
`:. color(darkviolet)(x=1, \ y=1)``x=1, y=1` -
Question 4 of 7
4. Question
Find the solution to the simultaneous equations by graphing.
`x+3y=15`
`y-x=1`
- `x=` (3) `y=` (4)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `x+3y=15`Make `y` the subject to get the equation of the line.`x+3y \ color(crimson)(-x)` `=` `15 \ color(crimson)(-x)` Add `-x` to both sides `3y \ cancel(+x) cancel(-x)` `=` `15 \ color(crimson)(-x)` `\ color(crimson)(3)y\ color(crimson)(\div(3))` `=` `(-x+15) \ color(crimson)(\div(3))` Divide both sides by `3` `y` `=` `-1/3x+5` Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `5` `14/3` `13/3` `4` Plot the points and draw the graph.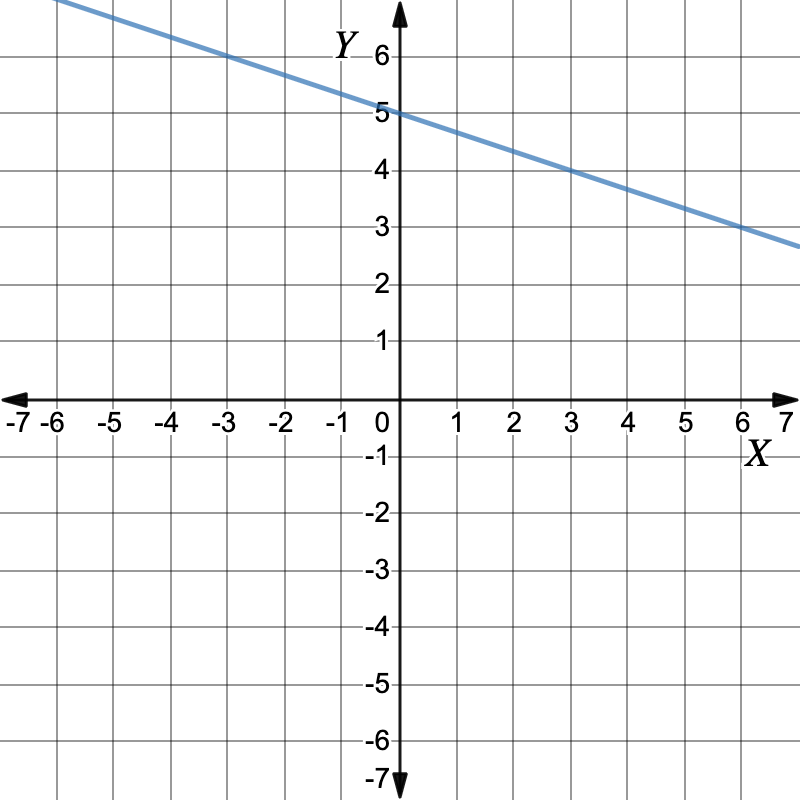
Graph: `y-x=1`First, make `y` the subject.`y-x` `=` `1` `y` `=` `x+1` Make `y` the subject Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `1` `2` `3` `4` Plot the points and draw the graph.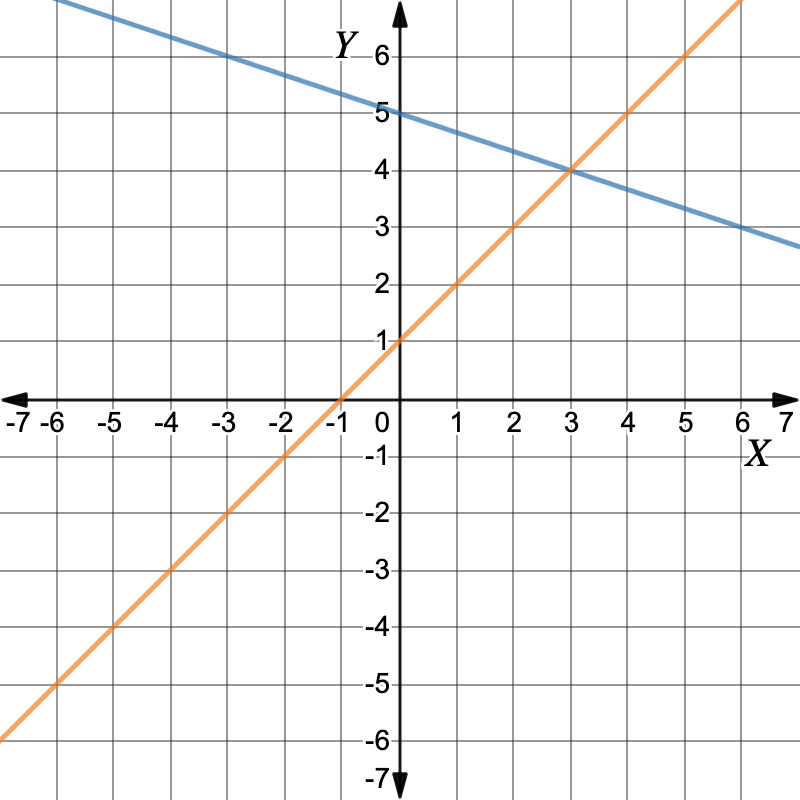
The graphs intersect at the point `(3,4)`
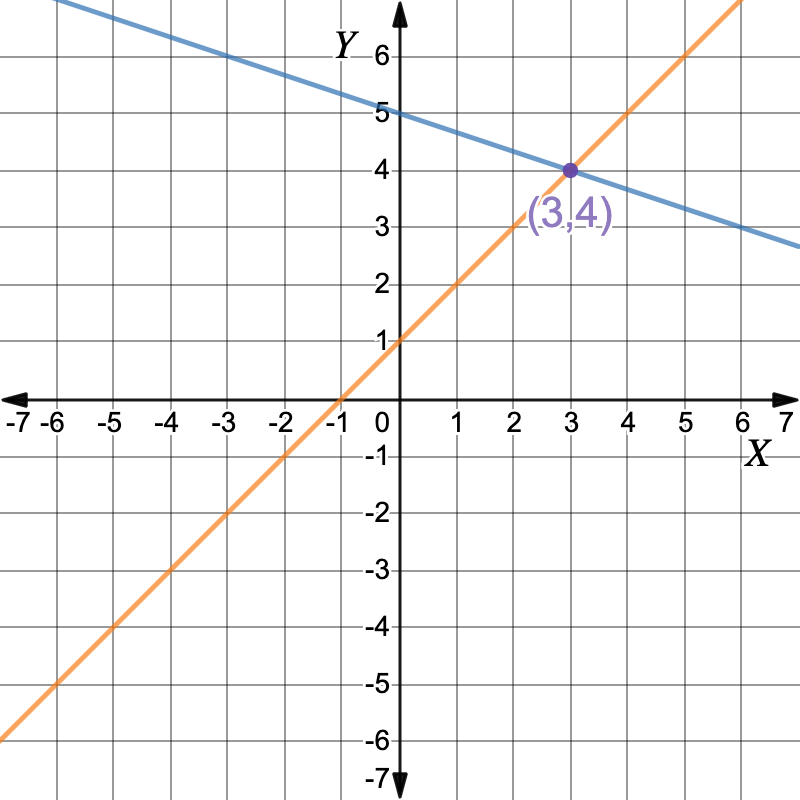`:. color(darkviolet)(x=3, \ y=4)``x=3, y=4` -
Question 5 of 7
5. Question
Find the solution to the simultaneous equations by graphing.
`2x+y=2`
`x+y=2`
- `x=` (0) `y=` (2)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `2x+y=2`Make `y` the subject to get the equation of the line.`2x+y \ color(crimson)(-2x)` `=` `2 \ color(crimson)(-2x)` Add `-2x` to both sides `y \ cancel(+2x) cancel(-2x)` `=` `2\ color(crimson)(-2x)` `y` `=` `-2x+2` Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `2` `0` `-2` `-4` Plot the points and draw the graph.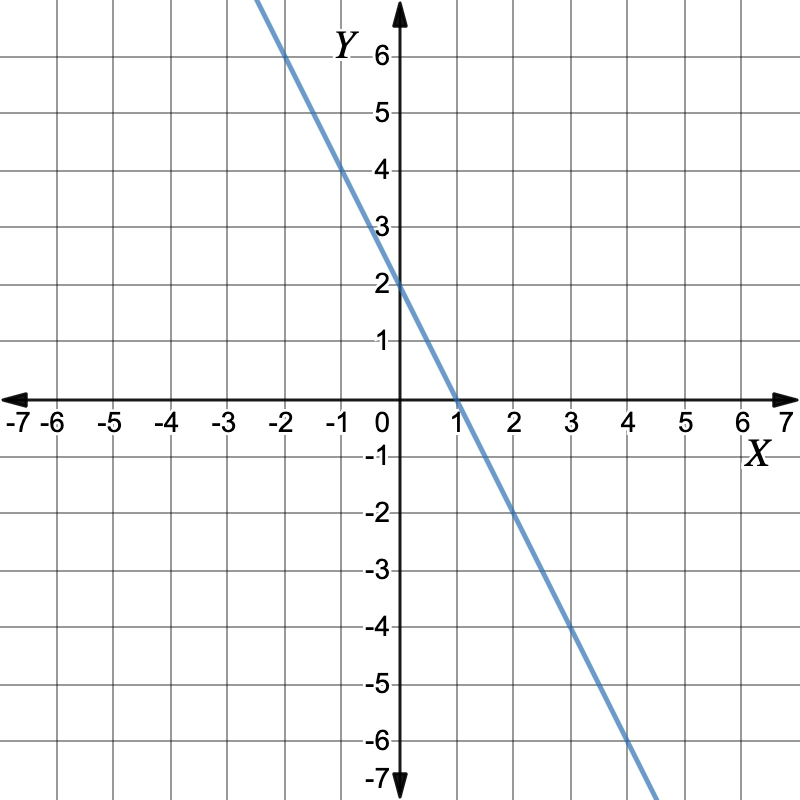
Graph: `x+y=2`First, make `y` the subject.`x+y` `=` `2` `y` `=` `-x+2` Make `y` the subject Working out the y-values for each x-value in the table of values.`x` `0` `1` `2` `3` `y` `2` `1` `0` `-1` Plot the points and draw the graph.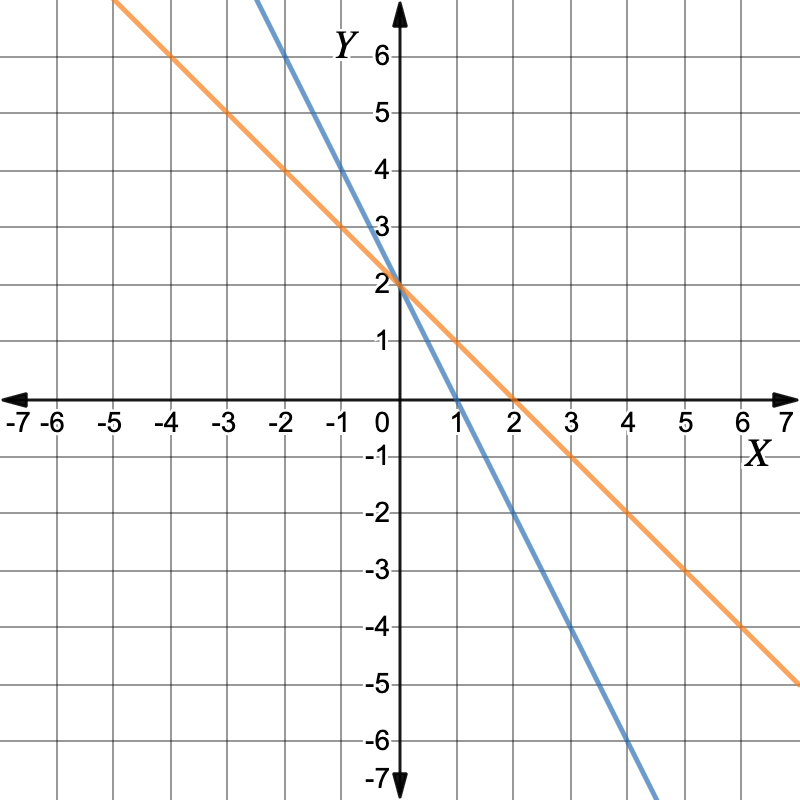
The graphs intersect at the point `(0,2)`
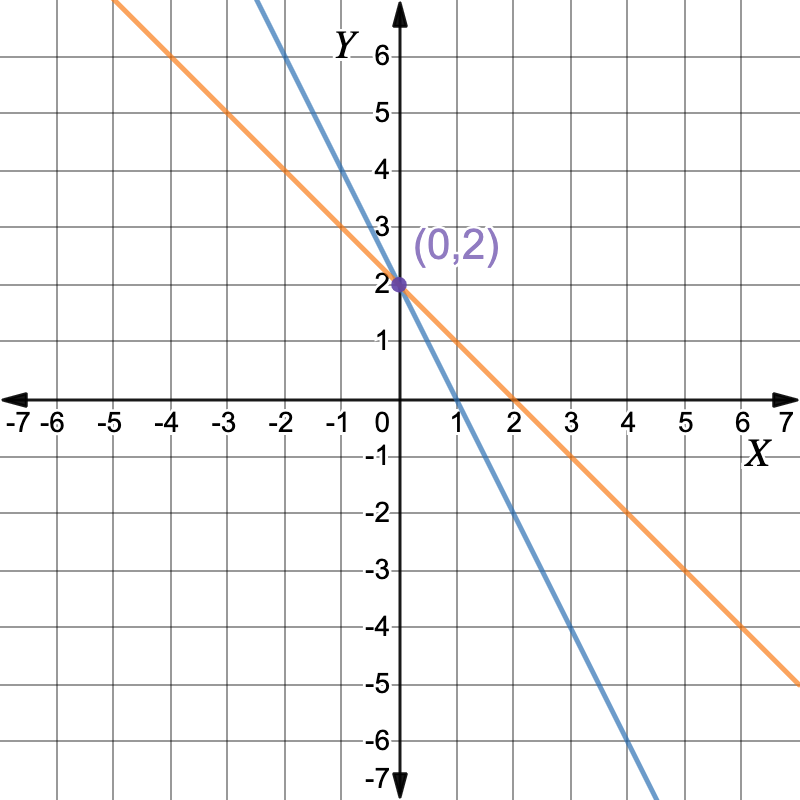`:. color(darkviolet)(x=0, \ y=2)``x=0, y=2` -
Question 6 of 7
6. Question
Find the solution to the simultaneous equations by graphing.
`y-x=4`
`x-y=1`
- `x=` (no solution) `y=` (no solution)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `y-x=4`Make `y` the subject to get the equation of the line.`y-x \ color(crimson)(+x)` `=` `4 \ color(crimson)(+x)` Add `x` to both sides `y \ cancel(-x) cancel(+x)` `=` `4 \ color(crimson)(+x)` `y` `=` `x+4` Working out the y-values for each x-value in the table of values.`x` `-2` `0` `2` `4` `y` `2` `4` `6` `8` Plot the points and draw the graph.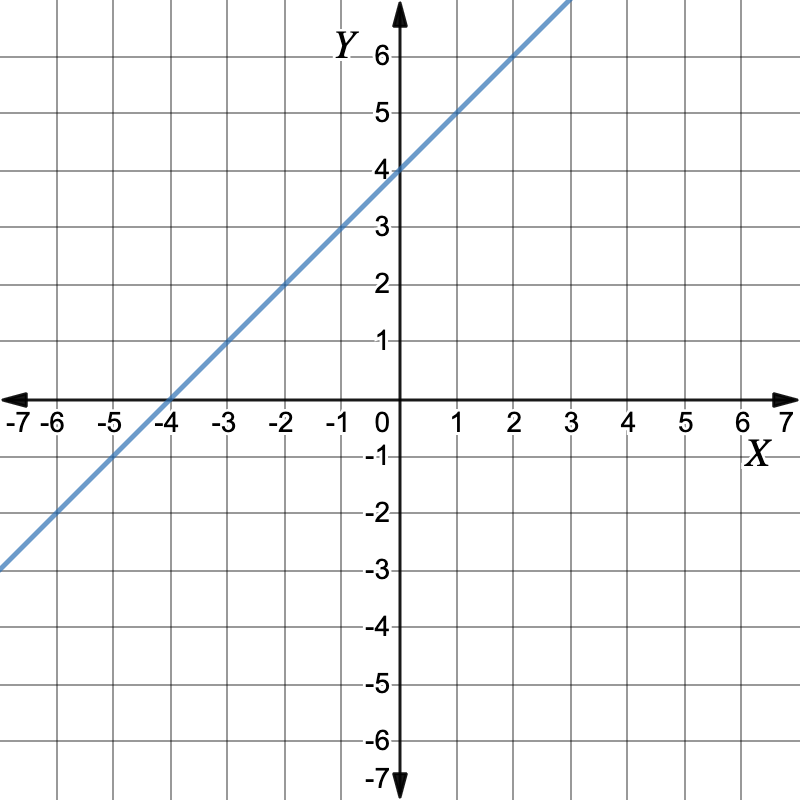
Graph: `x+y=1`First, make `y` the subject.`x-y` `=` `1` `y` `=` `x-1` Make `y` the subject Working out the y-values for each x-value in the table of values.`x` `-2` `0` `2` `4` `y` `-3` `-1` `1` `3` Plot the points and draw the graph.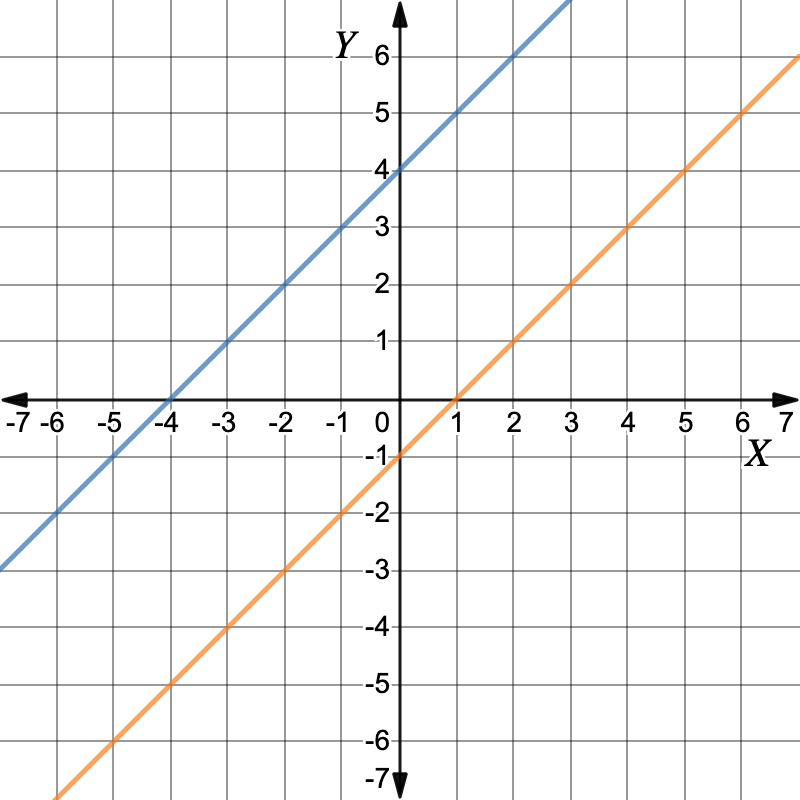
The graphs are parallel the lines do not intersect.There is no solution.There is no solution. -
Question 7 of 7
7. Question
Find the solution to the simultaneous equations by graphing.
`-6x+2y=8`
`y=3x+4`
- `x=` (infinite solutions) `y=` (infinite solutions)
Correct
Great Work!
Incorrect
First graph the equations.Graph: `-6x+2y=8`Make `y` the subject to get the equation of the line.`-6x+2y \ color(crimson)(+6x)` `=` `8 \ color(crimson)(+6x)` Add `6x` to both sides `2y \ cancel(-6x) cancel(+6x)` `=` `8 \ color(crimson)(+6x)` `\ color(crimson)(2)y\ color(crimson)(\div(2))` `=` `(6x+8) \ color(crimson)(\div(2))` Divide both sides by `2` `y` `=` `3x+4` Working out the y-values for each x-value in the table of values.`x` `-2` `-1` `0` `1` `y` `-2` `1` `4` `7` Plot the points and draw the graph.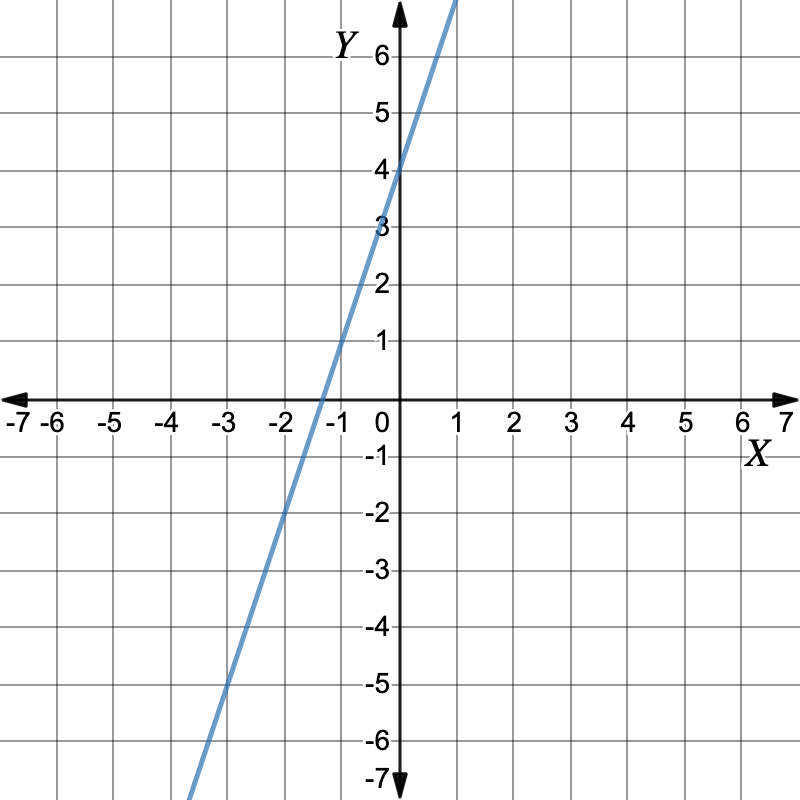
Graph: `y=3x+4`First, `y` is the subject.`y` `=` `3x+4` `y` is the subject Working out the y-values for each x-value in the table of values.`x` `-2` `-1` `0` `1` `y` `-2` `1` `4` `7` Plot the points and draw the graph.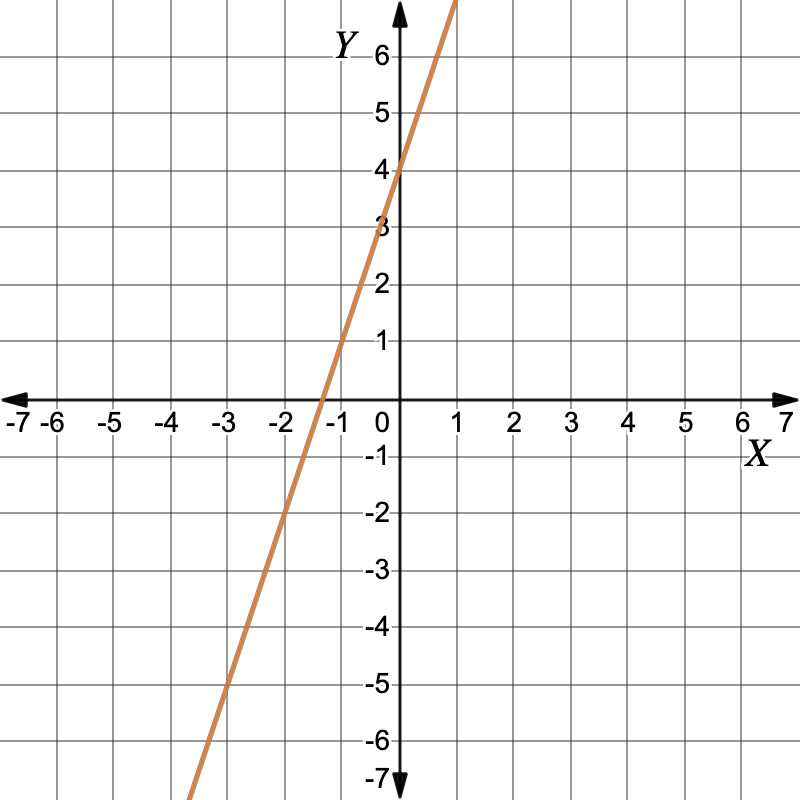
The graphs are both the same single line. This means there is an infinite number of solutions.Infinite solutionsInfinite solutions
Quizzes
- Solve Simultaneous Equations by Graphing
- Substitution Method 1
- Substitution Method 2
- Substitution Method 3
- Substitution Method 4
- Elimination Method 1
- Elimination Method 2
- Elimination Method 3
- Elimination Method 4
- Nonlinear Simultaneous Equations
- Simultaneous Equations Word Problems 1
- Simultaneous Equations Word Problems 2
- 3 Variable Simultaneous Equations – Substitution Method
- 3 Variable Simultaneous Equations – Elimination Method